

 In 1745 a new physics and mathematics professor at the University of Leyden
(spelled Leiden in modern Dutch), Pieter van Musschenbroek (1692 - 1791) and his assistants Allmand and
Cunaeus from the Netherlands invented the 'capacitor' (electro-static charge or capacitance actually) but did not
know it at first. His condenser was called the 'Leyden Jar' (pronounced: LY'duhn) and named so by Abbe Nollet. This
Leyden jar consisted of a narrow-necked glass jar coated over part of its inner and outer surfaces with a conductive
metallic substance; a conducting rod or wire passes through as insulating stopper (cork) in the neck of the jar and
contacts the inner foil layer, which is separated from the outer layer by the glass wall. The Leyden jar was one of
the first devices used to store an electric charge. If the inner layers of foil and outer layers of foil are then
connected by a conductor, their opposite charges will cause a spark that discharges the jar. Actually,
van Musschenbroek's very first 'condenser' was nothing more than a beer glass!
In 1745 a new physics and mathematics professor at the University of Leyden
(spelled Leiden in modern Dutch), Pieter van Musschenbroek (1692 - 1791) and his assistants Allmand and
Cunaeus from the Netherlands invented the 'capacitor' (electro-static charge or capacitance actually) but did not
know it at first. His condenser was called the 'Leyden Jar' (pronounced: LY'duhn) and named so by Abbe Nollet. This
Leyden jar consisted of a narrow-necked glass jar coated over part of its inner and outer surfaces with a conductive
metallic substance; a conducting rod or wire passes through as insulating stopper (cork) in the neck of the jar and
contacts the inner foil layer, which is separated from the outer layer by the glass wall. The Leyden jar was one of
the first devices used to store an electric charge. If the inner layers of foil and outer layers of foil are then
connected by a conductor, their opposite charges will cause a spark that discharges the jar. Actually,
van Musschenbroek's very first 'condenser' was nothing more than a beer glass! By modern standards, the Leyden jar is cumbersome and inefficient. It is rarely used except in exciting laboratory
demonstrations of capacitance, and exiting they are! Benjamin Franklin was acquainted with the Leyden Jar experiments
also so he decided to test his ideas that 'charge' could also be caused by thunder and lightning. Franklin tested his
theories, in Philadelphia in June 1752, via his now famous 'Electrical Fluid Theory' to prove that lightning was an
electrical phenomenon. What he did was fly a kite which had a metal tip.
The kite was tied with wet conducting thin hemp cord and at the end he
attached a metal key to which a non-conducting silk string was attached which he held in his hand; when he held his
knuckles near the key he could draw sparks from it. Although his experiment was completed successfully and the results
as he had calculated before, the next couple people after him who tried the hazardous experiment were killed by
lightning strikes. I guess Franklin was extremely lucky with his hazardous experiments. I myself believe in some sort
of "time-line" in which inventions are invented 'no matter what'.
By modern standards, the Leyden jar is cumbersome and inefficient. It is rarely used except in exciting laboratory
demonstrations of capacitance, and exiting they are! Benjamin Franklin was acquainted with the Leyden Jar experiments
also so he decided to test his ideas that 'charge' could also be caused by thunder and lightning. Franklin tested his
theories, in Philadelphia in June 1752, via his now famous 'Electrical Fluid Theory' to prove that lightning was an
electrical phenomenon. What he did was fly a kite which had a metal tip.
The kite was tied with wet conducting thin hemp cord and at the end he
attached a metal key to which a non-conducting silk string was attached which he held in his hand; when he held his
knuckles near the key he could draw sparks from it. Although his experiment was completed successfully and the results
as he had calculated before, the next couple people after him who tried the hazardous experiment were killed by
lightning strikes. I guess Franklin was extremely lucky with his hazardous experiments. I myself believe in some sort
of "time-line" in which inventions are invented 'no matter what'.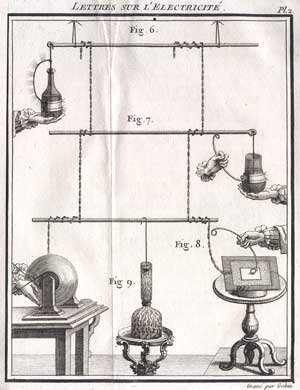 Look at the picture at the right; the worlds first illustration of the working of a Leyden Jar, by Abbe
Jean-Antoine Nollet!
Look at the picture at the right; the worlds first illustration of the working of a Leyden Jar, by Abbe
Jean-Antoine Nollet!
 What exactly is a 'Capacitor'?
A capacitor is a device that stores an electrical charge or energy on it's plates. These plates (see Fig. 1),
a positive and a negative plate, are placed very close together with an insulator in between to prevent the plates
from touching each other. A capacitor can carry a voltage equal to the battery or input voltage. Usually a
capacitor has more than two plates depending on the capacitance or dielectric type.
What exactly is a 'Capacitor'?
A capacitor is a device that stores an electrical charge or energy on it's plates. These plates (see Fig. 1),
a positive and a negative plate, are placed very close together with an insulator in between to prevent the plates
from touching each other. A capacitor can carry a voltage equal to the battery or input voltage. Usually a
capacitor has more than two plates depending on the capacitance or dielectric type.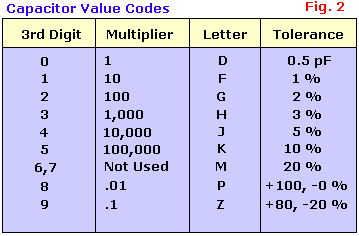
 Electrolytic - Made of electrolyte, basically conductive salt
in solvent. Aluminum electrodes are used by using a thin oxidation membrane. Most common type, polarized capacitor.
Applications: Ripple filters, timing circuits. Cheap, readily available, good for storage of charge (energy). Not
very accurate, marginal electrical properties, leakage, drifting, not suitable for use in hf circuits, available in
very
small or very large values in uF. They WILL explode if the rated working voltage is exceeded or polarity is
reversed, so be careful. When you use this type capacitor in one of your projects, the rule-of-thumb is to choose one
which is twice the supply voltage. Example, if your supply power is 12 volt you would choose a 24volt (25V) type.
This type has come a long way and characteristics have constantly improved over the years. It is and always will be
an all-time favorite; unless something better comes along to replace it. But I don't think so for this decade; polarized
capacitors are heavily used in almost every kind of equipment and consumer electronics.
Electrolytic - Made of electrolyte, basically conductive salt
in solvent. Aluminum electrodes are used by using a thin oxidation membrane. Most common type, polarized capacitor.
Applications: Ripple filters, timing circuits. Cheap, readily available, good for storage of charge (energy). Not
very accurate, marginal electrical properties, leakage, drifting, not suitable for use in hf circuits, available in
very
small or very large values in uF. They WILL explode if the rated working voltage is exceeded or polarity is
reversed, so be careful. When you use this type capacitor in one of your projects, the rule-of-thumb is to choose one
which is twice the supply voltage. Example, if your supply power is 12 volt you would choose a 24volt (25V) type.
This type has come a long way and characteristics have constantly improved over the years. It is and always will be
an all-time favorite; unless something better comes along to replace it. But I don't think so for this decade; polarized
capacitors are heavily used in almost every kind of equipment and consumer electronics. Tantalum - Made of Tantalum Pentoxide. They are electrolytic
capacitors but used with a material called tantalum for the electrodes. Superior to electrolytic capacitors,
excellent temperature and frequency characteristics. When tantalum powder is baked in order to solidify it, a crack
forms inside. An electric charge can be stored on this crack. Like electrolytics, tantalums are polarized so watch the
'+' and '-' indicators. Mostly used in analog signal systems because of the lack of current-spike-noise. Small size
fits anywhere, reliable, most common values readily available. Expensive, easily damaged by spikes, large values
exists but may be hard to obtain. Largest in my own collection is 220uF/35V, beige color.
Tantalum - Made of Tantalum Pentoxide. They are electrolytic
capacitors but used with a material called tantalum for the electrodes. Superior to electrolytic capacitors,
excellent temperature and frequency characteristics. When tantalum powder is baked in order to solidify it, a crack
forms inside. An electric charge can be stored on this crack. Like electrolytics, tantalums are polarized so watch the
'+' and '-' indicators. Mostly used in analog signal systems because of the lack of current-spike-noise. Small size
fits anywhere, reliable, most common values readily available. Expensive, easily damaged by spikes, large values
exists but may be hard to obtain. Largest in my own collection is 220uF/35V, beige color. Super Capacitors - The Electric Double Layer capacitor is
a real miracle piece of work. Capacitance is 0.47 Farad (470,000 uF). Despite the large capacitance value, its
physical dimensions are relatively small. It has a diameter of 21 mm (almost an inch) and a height of 11 mm (1/2 inch).
Like other electrolytics the super capacitor is also polarized so exercise caution in regards to the break-down voltage.
Care must be taken when using this capacitor. It has such large capacitance that, without precautions, it would destroy
part of a powersupply such as the bridge rectifier, volt regulators, or whatever because of the huge inrush current at
charge. For a brief moment, this capacitor acts like a short circuit when the capacitor is charged. Protection
circuitry is a must for this type.
Super Capacitors - The Electric Double Layer capacitor is
a real miracle piece of work. Capacitance is 0.47 Farad (470,000 uF). Despite the large capacitance value, its
physical dimensions are relatively small. It has a diameter of 21 mm (almost an inch) and a height of 11 mm (1/2 inch).
Like other electrolytics the super capacitor is also polarized so exercise caution in regards to the break-down voltage.
Care must be taken when using this capacitor. It has such large capacitance that, without precautions, it would destroy
part of a powersupply such as the bridge rectifier, volt regulators, or whatever because of the huge inrush current at
charge. For a brief moment, this capacitor acts like a short circuit when the capacitor is charged. Protection
circuitry is a must for this type. Polyester Film - This capacitor uses a thin polyester
film as a dielectric. Not as high a tolerance as polypropylene, but cheap, temperature stable, readily available,
widely used. Tolerance is approx 5% to 10%. Can be quite large depending on capacity or rated voltage and so may
not be suitable for all applications.
Polyester Film - This capacitor uses a thin polyester
film as a dielectric. Not as high a tolerance as polypropylene, but cheap, temperature stable, readily available,
widely used. Tolerance is approx 5% to 10%. Can be quite large depending on capacity or rated voltage and so may
not be suitable for all applications. Polypropylene - Mainly used when a higher tolerance
is needed then polyester caps can offer. This polypropylene film is the dielectric.
Polypropylene - Mainly used when a higher tolerance
is needed then polyester caps can offer. This polypropylene film is the dielectric. Polystyrene - Is used as a
dielectric. Constructed like a coil inside so not suitable for high frequency applications. Well used in filter
circuits or timing applications using a couple hundred KHz or less. Electrodes may be reddish of color because of
copper leaf used or silver when aluminum foil is used for electrodes.
Polystyrene - Is used as a
dielectric. Constructed like a coil inside so not suitable for high frequency applications. Well used in filter
circuits or timing applications using a couple hundred KHz or less. Electrodes may be reddish of color because of
copper leaf used or silver when aluminum foil is used for electrodes. Metalized Polyester Film - Dielectric
made of Polyester or DuPont trade name "Mylar". Good quality, low drift, temperature stable. Because the electrodes
are thin they can be made very very small. Good all-round capacitor.
Metalized Polyester Film - Dielectric
made of Polyester or DuPont trade name "Mylar". Good quality, low drift, temperature stable. Because the electrodes
are thin they can be made very very small. Good all-round capacitor. Epoxy - Manufactured using an epoxy
dipped polymers as a protective coating. Widely available, stable, cheap. Can be quite large depending on capacity or
rated voltage and so may not be suitable for all applications.
Epoxy - Manufactured using an epoxy
dipped polymers as a protective coating. Widely available, stable, cheap. Can be quite large depending on capacity or
rated voltage and so may not be suitable for all applications. Ceramic - Constructed with materials such as titanium acid
barium for dielectric. Internally these capacitors are not constructed as a coil, so they are well suited for use in
high frequency applications. Typically used to by-pass high frequency signals to ground. They are shaped like a disk,
available in very small capacitance values and very small sizes. Together with the electrolytics the most widely available
and used capacitor around. Comes in very small size and value, very cheap, reliable. Subject to drifting depending
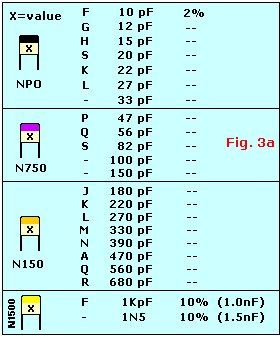
on ambient temperature. NPO types are the temperature stable types. They are identified by a black stripe on top.
Ceramic - Constructed with materials such as titanium acid
barium for dielectric. Internally these capacitors are not constructed as a coil, so they are well suited for use in
high frequency applications. Typically used to by-pass high frequency signals to ground. They are shaped like a disk,
available in very small capacitance values and very small sizes. Together with the electrolytics the most widely available
and used capacitor around. Comes in very small size and value, very cheap, reliable. Subject to drifting depending
on ambient temperature. NPO types are the temperature stable types. They are identified by a black stripe on top. Multilayer Ceramic - Dielectric is made up
of many layers. Small in size, very good temperature stability, excellent frequency stable characteristics. Used in
applications to filter or bypass the high frequency to ground. They don't have a polarity. *Multilayer caps suffer from
high-Q internal (parallel) resonances - generally in the VHF range. The CK05 style 0.1uF/50V caps for example
resonate around 30MHz. The effect of this resonance is effectively no apparent capacitance near the resonant frequency.
Multilayer Ceramic - Dielectric is made up
of many layers. Small in size, very good temperature stability, excellent frequency stable characteristics. Used in
applications to filter or bypass the high frequency to ground. They don't have a polarity. *Multilayer caps suffer from
high-Q internal (parallel) resonances - generally in the VHF range. The CK05 style 0.1uF/50V caps for example
resonate around 30MHz. The effect of this resonance is effectively no apparent capacitance near the resonant frequency. Silver-Mica - Mica is used as a dielectric. Used in
resonance circuits, frequency filters, and military RF applications.
Silver-Mica - Mica is used as a dielectric. Used in
resonance circuits, frequency filters, and military RF applications. Adjustable Capacitors - Also called
trimmer capacitors or variable capacitors. It uses ceramic or plastic as a dielectric.
Adjustable Capacitors - Also called
trimmer capacitors or variable capacitors. It uses ceramic or plastic as a dielectric. Tuning or 'air-core' capacitors.
Tuning or 'air-core' capacitors.
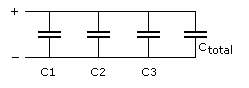 Capacitors connected in parallel, which is the most desirable,
have their capacitance added together, which is just the opposite of parallel resistors. It is an excellent way of
increasing the total storage capacity of an electric charge:
Capacitors connected in parallel, which is the most desirable,
have their capacitance added together, which is just the opposite of parallel resistors. It is an excellent way of
increasing the total storage capacity of an electric charge: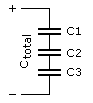
| microFarads (�F) | nanoFarads (nF) | picoFarads (pF) | ||
| 0.000001�F | = | 0.001nF | = | 1pF |
| 0.00001�F | = | 0.01nF | = | 10pF |
| 0.0001�F | = | 0.1nF | = | 100pF |
| 0.001�F | = | 1nF | = | 1000pF |
| 0.01�F | = | 10nF | = | 10,000pF |
| 0.1�F | = | 100nF | = | 100,000pF |
| 1�F | = | 1000nF | = | 1,000,000pF |
| 10�F | = | 10,000nF | = | 10,000,000pF |
| 100�F | = | 100,000nF | = | 100,000,000pF |
Table 1. Capacitance Conversion
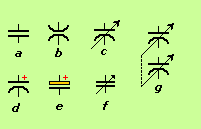 Capacitors in Schematics:
Capacitors in Schematics:
Metric Prefix Symbol Power of 10 (multiplier)
giga [Note 2] G x 10^9
mega M x 10^6
kilo K x 10^3
(none) x 10^0 (same as 1 or unity)
milli m x 10^-3
micro f x 10^-6
nano n x 10^-9
pico p x 10^-12
This list does extend farther in either direction, but those larger and smaller multipliers are not as commonly used
in electronics. But using this list, you'll find that the common capacitor multipliers in the United States will be f
(micro) and p (pico). A capacitor with a value of 3.3fF is the same as a capacitor with a value of 3.3 x 10^-6 farads
or 0.0000033 farads. "f", by the way, is the lower-case Greek letter "mu", properly written as our Roman lower case
"u" with a leading descender much as a "y" has a trailing descender.68 mF 68 MF 68 mfd 68 MFDIt was always understood that "mF", "MF", "mfd" or "MFD" ALWAYS meant microfarad. Microfarad or micromicrofarad were the only units used for capacitors back then, so no one would ever even consider that "mfd" might mean "millifarad" or that "MFD" might mean "megafarad"! Even today, you'll still see "MFD" on capacitors, especially on motor start or motor run capacitors.
B = ±0.1pF
C = ±0.25pF
D = ±0.5pF
E = ±0.25%
F = ±1.0%
G = ±2%
H = ±2.5%
J = ±5% *
K = ±10% *
L = ±15%
M = ±20% *
N = ±30%
P = -0, +100%
S = -20, +50%
W = -0, +200%
X = -20, +40%
Z = -20, +80% *
You'll find that the "Z" tolerance of -20, +80% to be common for aluminum electrolytic caps and for disc ceramic
caps that are used for what is known as "bulk capacitance" in applications such as power supply bypassing or filtering.
These kinds of capacitors are used where it's OK for the value to be a lot larger than nominal, but they don't want it
to go very far below that value. 1E 25V
1H 50V
2A 100V
Since this seems to be European in nature, these voltage markings are new territory for me. I would appreciate more
information on this so that I can flesh out this article and make it more accurate. My e-mail address appears in the
"Wrapup" section following in case you would like to contact me with some of this information. I try to be accurate,
so please make sure that you include source material rather than depending upon hand-me-down folklore!



