Learning Electronics

Learning Electronics

Learn to build electronic circuits
Volume II - AC » BASIC AC THEORY

AC waveforms

When an alternator produces AC voltage, the voltage switches polarity over time, but does so in a very particular manner. When graphed over time, the “wave” traced by this voltage of alternating polarity from an alternator takes on a distinct shape, known as a sine wave: Figure below

Graph of AC voltage over time (the sine wave).

In the voltage plot from an electromechanical alternator, the change from one polarity to the other is a smooth one, the voltage level changing most rapidly at the zero (“crossover”) point and most slowly at its peak. If we were to graph the trigonometric function of “sine” over a horizontal range of 0 to 360 degrees, we would find the exact same pattern as in Table below.

Trigonometric “sine” function.
Angle (o) sin(angle) wave Angle (o) sin(angle) wave
0 0.0000 zero 180 0.0000 zero
15 0.2588 + 195 -0.2588 -
30 0.5000 + 210 -0.5000 -
45 0.7071 + 225 -0.7071 -
60 0.8660 + 240 -0.8660 -
75 0.9659 + 255 -0.9659 -
90 1.0000 +peak 270 -1.0000 -peak
105 0.9659 + 285 -0.9659 -
120 0.8660 + 300 -0.8660 -
135 0.7071 + 315 -0.7071 -
150 0.5000 + 330 -0.5000 -
165 0.2588 + 345 -0.2588 -
180 0.0000 zero 360 0.0000 zero


The reason why an electromechanical alternator outputs sine-wave AC is due to the physics of its operation. The voltage produced by the stationary coils by the motion of the rotating magnet is proportional to the rate at which the magnetic flux is changing perpendicular to the coils (Faraday's Law of Electromagnetic Induction). That rate is greatest when the magnet poles are closest to the coils, and least when the magnet poles are furthest away from the coils. Mathematically, the rate of magnetic flux change due to a rotating magnet follows that of a sine function, so the voltage produced by the coils follows that same function.

If we were to follow the changing voltage produced by a coil in an alternator from any point on the sine wave graph to that point when the wave shape begins to repeat itself, we would have marked exactly one cycle of that wave. This is most easily shown by spanning the distance between identical peaks, but may be measured between any corresponding points on the graph. The degree marks on the horizontal axis of the graph represent the domain of the trigonometric sine function, and also the angular position of our simple two-pole alternator shaft as it rotates: Figure below

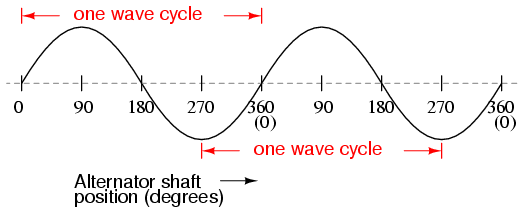
Alternator voltage as function of shaft position (time).

Since the horizontal axis of this graph can mark the passage of time as well as shaft position in degrees, the dimension marked for one cycle is often measured in a unit of time, most often seconds or fractions of a second. When expressed as a measurement, this is often called the period of a wave. The period of a wave in degrees is always 360, but the amount of time one period occupies depends on the rate voltage oscillates back and forth.

A more popular measure for describing the alternating rate of an AC voltage or current wave than period is the rate of that back-and-forth oscillation. This is called frequency. The modern unit for frequency is the Hertz (abbreviated Hz), which represents the number of wave cycles completed during one second of time. In the United States of America, the standard power-line frequency is 60 Hz, meaning that the AC voltage oscillates at a rate of 60 complete back-and-forth cycles every second. In Europe, where the power system frequency is 50 Hz, the AC voltage only completes 50 cycles every second. A radio station transmitter broadcasting at a frequency of 100 MHz generates an AC voltage oscillating at a rate of 100 million cycles every second.

Prior to the canonization of the Hertz unit, frequency was simply expressed as “cycles per second.” Older meters and electronic equipment often bore frequency units of “CPS” (Cycles Per Second) instead of Hz. Many people believe the change from self-explanatory units like CPS to Hertz constitutes a step backward in clarity. A similar change occurred when the unit of “Celsius” replaced that of “Centigrade” for metric temperature measurement. The name Centigrade was based on a 100-count (“Centi-”) scale (“-grade”) representing the melting and boiling points of H2O, respectively. The name Celsius, on the other hand, gives no hint as to the unit's origin or meaning.

Period and frequency are mathematical reciprocals of one another. That is to say, if a wave has a period of 10 seconds, its frequency will be 0.1 Hz, or 1/10 of a cycle per second:

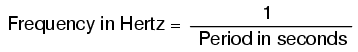
An instrument called an oscilloscope, Figure below, is used to display a changing voltage over time on a graphical screen. You may be familiar with the appearance of an ECG or EKG (electrocardiograph) machine, used by physicians to graph the oscillations of a patient's heart over time. The ECG is a special-purpose oscilloscope expressly designed for medical use. General-purpose oscilloscopes have the ability to display voltage from virtually any voltage source, plotted as a graph with time as the independent variable. The relationship between period and frequency is very useful to know when displaying an AC voltage or current waveform on an oscilloscope screen. By measuring the period of the wave on the horizontal axis of the oscilloscope screen and reciprocating that time value (in seconds), you can determine the frequency in Hertz.

Time period of sinewave is shown on oscilloscope.

Voltage and current are by no means the only physical variables subject to variation over time. Much more common to our everyday experience is sound, which is nothing more than the alternating compression and decompression (pressure waves) of air molecules, interpreted by our ears as a physical sensation. Because alternating current is a wave phenomenon, it shares many of the properties of other wave phenomena, like sound. For this reason, sound (especially structured music) provides an excellent analogy for relating AC concepts.

In musical terms, frequency is equivalent to pitch. Low-pitch notes such as those produced by a tuba or bassoon consist of air molecule vibrations that are relatively slow (low frequency). High-pitch notes such as those produced by a flute or whistle consist of the same type of vibrations in the air, only vibrating at a much faster rate (higher frequency). Figure below is a table showing the actual frequencies for a range of common musical notes.

The frequency in Hertz (Hz) is shown for various musical notes.

Astute observers will notice that all notes on the table bearing the same letter designation are related by a frequency ratio of 2:1. For example, the first frequency shown (designated with the letter “A”) is 220 Hz. The next highest “A” note has a frequency of 440 Hz -- exactly twice as many sound wave cycles per second. The same 2:1 ratio holds true for the first A sharp (233.08 Hz) and the next A sharp (466.16 Hz), and for all note pairs found in the table.

Audibly, two notes whose frequencies are exactly double each other sound remarkably similar. This similarity in sound is musically recognized, the shortest span on a musical scale separating such note pairs being called an octave. Following this rule, the next highest “A” note (one octave above 440 Hz) will be 880 Hz, the next lowest “A” (one octave below 220 Hz) will be 110 Hz. A view of a piano keyboard helps to put this scale into perspective: Figure below

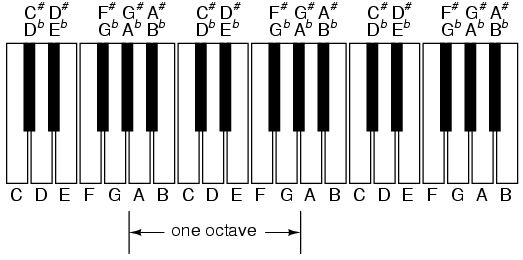
An octave is shown on a musical keyboard.

As you can see, one octave is equal to seven white keys' worth of distance on a piano keyboard. The familiar musical mnemonic (doe-ray-mee-fah-so-lah-tee) -- yes, the same pattern immortalized in the whimsical Rodgers and Hammerstein song sung in The Sound of Music -- covers one octave from C to C.

While electromechanical alternators and many other physical phenomena naturally produce sine waves, this is not the only kind of alternating wave in existence. Other “waveforms” of AC are commonly produced within electronic circuitry. Here are but a few sample waveforms and their common designations in figure below

Some common waveshapes (waveforms).

These waveforms are by no means the only kinds of waveforms in existence. They're simply a few that are common enough to have been given distinct names. Even in circuits that are supposed to manifest “pure” sine, square, triangle, or sawtooth voltage/current waveforms, the real-life result is often a distorted version of the intended waveshape. Some waveforms are so complex that they defy classification as a particular “type” (including waveforms associated with many kinds of musical instruments). Generally speaking, any waveshape bearing close resemblance to a perfect sine wave is termed sinusoidal, anything different being labeled as non-sinusoidal. Being that the waveform of an AC voltage or current is crucial to its impact in a circuit, we need to be aware of the fact that AC waves come in a variety of shapes.

«Previous Page | Next Page»