Simple series resonance

A similar effect happens in series inductive/capacitive circuits. (Figure below) When a state of resonance is reached (capacitive and inductive reactances equal), the two impedances cancel each other out and the total impedance drops to zero!

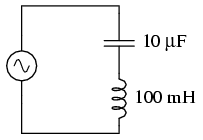
Simple series resonant circuit.

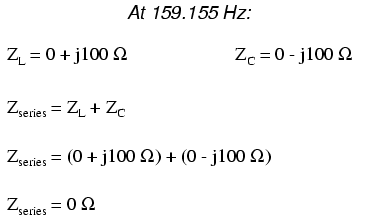
With the total series impedance equal to 0 Ω at the resonant frequency of 159.155 Hz, the result is a short circuit across the AC power source at resonance. In the circuit drawn above, this would not be good. I'll add a small resistor (Figure below) in series along with the capacitor and the inductor to keep the maximum circuit current somewhat limited, and perform another SPICE analysis over the same range of frequencies: (Figure below)

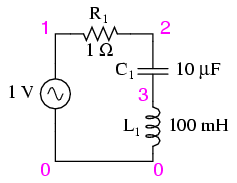
Series resonant circuit suitable for SPICE.

series lc circuit
v1 1 0 ac 1 sin 
r1 1 2 1
c1 2 3 10u      
l1 3 0 100m     
.ac lin 20 100 200      
.plot ac i(v1)  
.end    

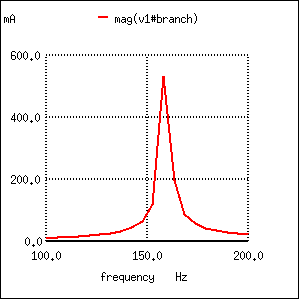
Series resonant circuit plot of current I(v1).

As before, circuit current amplitude increases from bottom to top, while frequency increases from left to right. (Figure above) The peak is still seen to be at the plotted frequency point of 157.9 Hz, the closest analyzed point to our predicted resonance point of 159.155 Hz. This would suggest that our resonant frequency formula holds as true for simple series LC circuits as it does for simple parallel LC circuits, which is the case:

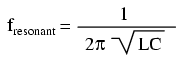
A word of caution is in order with series LC resonant circuits: because of the high currents which may be present in a series LC circuit at resonance, it is possible to produce dangerously high voltage drops across the capacitor and the inductor, as each component possesses significant impedance. We can edit the SPICE netlist in the above example to include a plot of voltage across the capacitor and inductor to demonstrate what happens: (Figure below)

series lc circuit   
v1 1 0 ac 1 sin 
r1 1 2 1
c1 2 3 10u      
l1 3 0 100m     
.ac lin 20 100 200      
.plot ac i(v1) v(2,3) v(3)      
.end    

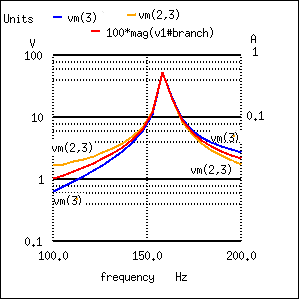
Plot of Vc=V(2,3) 70 V peak, V_L=v(3) 70 V peak, I=I(V1#branch) 0.532 A peak

According to SPICE, voltage across the capacitor and inductor reach a peak somewhere around 70 volts! This is quite impressive for a power supply that only generates 1 volt. Needless to say, caution is in order when experimenting with circuits such as this. This SPICE voltage is lower than the expected value due to the small (20) number of steps in the AC analysis statement (.ac lin 20 100 200). What is the expected value?

    Given: fr = 159.155 Hz, L = 100mH, R = 1
           XL = 2πfL = 2π(159.155)(100mH)=j100Ω
           XC = 1/(2πfC) = 1/(2π(159.155)(10µF)) = -j100Ω
           Z = 1 +j100 -j100 = 1 Ω
           I = V/Z = (1 V)/(1 Ω) = 1 A
           VL = IZ = (1 A)(j100) = j100 V
           VC = IZ = (1 A)(-j100) = -j100 V
           VR = IR = (1 A)(1)= 1 V
           Vtotal = VL + VC + VR 
           Vtotal = j100 -j100 +1 = 1 V

The expected values for capacitor and inductor voltage are 100 V. This voltage will stress these components to that level and they must be rated accordingly. However, these voltages are out of phase and cancel yielding a total voltage across all three components of only 1 V, the applied voltage. The ratio of the capacitor (or inductor) voltage to the applied voltage is the “Q” factor.

           Q = VL/VR = VC/VR  

• REVIEW:
• The total impedance of a series LC circuit approaches zero as the power supply frequency approaches resonance.
• The same formula for determining resonant frequency in a simple tank circuit applies to simple series circuits as well.
• Extremely high voltages can be formed across the individual components of series LC circuits at resonance, due to high current flows and substantial individual component impedances.