DeMorgan's Theorems
A mathematician named DeMorgan developed a pair of important rules regarding group complementation in Boolean algebra. By group complementation, I'm referring to the complement of a group of terms, represented by a long bar over more than one variable.
You should recall from the chapter on logic gates that inverting all inputs to a gate reverses that gate's essential function from AND to OR, or vice versa, and also inverts the output. So, an OR gate with all inputs inverted (a Negative-OR gate) behaves the same as a NAND gate, and an AND gate with all inputs inverted (a Negative-AND gate) behaves the same as a NOR gate. DeMorgan's theorems state the same equivalence in "backward" form: that inverting the output of any gate results in the same function as the opposite type of gate (AND vs. OR) with inverted inputs:

A long bar extending over the term AB acts as a grouping symbol, and as such is entirely different from the product of A and B independently inverted. In other words, (AB)' is not equal to A'B'. Because the "prime" symbol (') cannot be stretched over two variables like a bar can, we are forced to use parentheses to make it apply to the whole term AB in the previous sentence. A bar, however, acts as its own grouping symbol when stretched over more than one variable. This has profound impact on how Boolean expressions are evaluated and reduced, as we shall see.
DeMorgan's theorem may be thought of in terms of breaking a long bar symbol. When a long bar is broken, the operation directly underneath the break changes from addition to multiplication, or vice versa, and the broken bar pieces remain over the individual variables. To illustrate:

When multiple "layers" of bars exist in an expression, you may only break one bar at a time, and it is generally easier to begin simplification by breaking the longest (uppermost) bar first. To illustrate, let's take the expression (A + (BC)')' and reduce it using DeMorgan's Theorems:
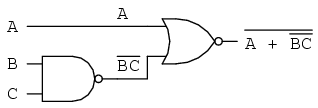
Following the advice of breaking the longest (uppermost) bar first, I'll begin by breaking the bar covering the entire expression as a first step:
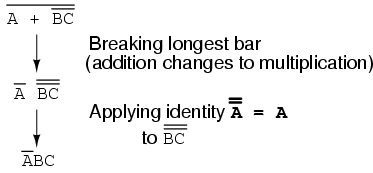
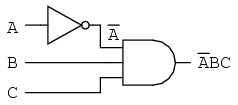
As a result, the original circuit is reduced to a three-input AND gate with the A input inverted:
You should never break more than one bar in a single step, as illustrated here:
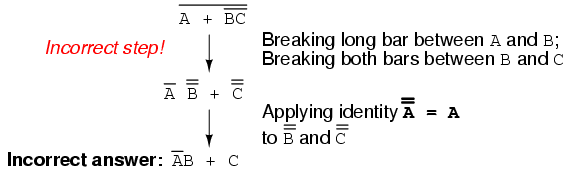
As tempting as it may be to conserve steps and break more than one bar at a time, it often leads to an incorrect result, so don't do it!
It is possible to properly reduce this expression by breaking the short bar first, rather than the long bar first:

The end result is the same, but more steps are required compared to using the first method, where the longest bar was broken first. Note how in the third step we broke the long bar in two places. This is a legitimate mathematical operation, and not the same as breaking two bars in one step! The prohibition against breaking more than one bar in one step is not a prohibition against breaking a bar in more than one place. Breaking in more than one place in a single step is okay; breaking more than one bar in a single step is not.
You might be wondering why parentheses were placed around the sub-expression B' + C', considering the fact that I just removed them in the next step. I did this to emphasize an important but easily neglected aspect of DeMorgan's theorem. Since a long bar functions as a grouping symbol, the variables formerly grouped by a broken bar must remain grouped lest proper precedence (order of operation) be lost. In this example, it really wouldn't matter if I forgot to put parentheses in after breaking the short bar, but in other cases it might. Consider this example, starting with a different expression:
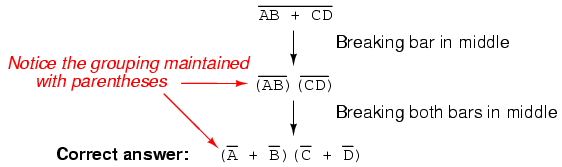
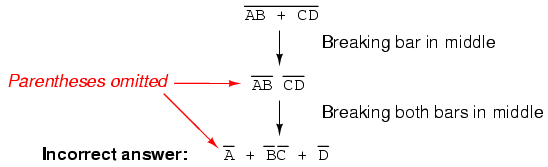
As you can see, maintaining the grouping implied by the complementation bars for this expression is crucial to obtaining the correct answer.
Let's apply the principles of DeMorgan's theorems to the simplification of a gate circuit:
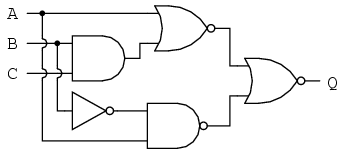
As always, our first step in simplifying this circuit must be to generate an equivalent Boolean expression. We can do this by placing a sub-expression label at the output of each gate, as the inputs become known. Here's the first step in this process:
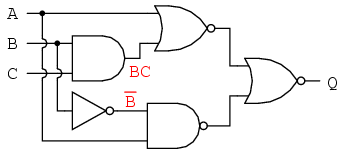
Next, we can label the outputs of the first NOR gate and the NAND gate. When dealing with inverted-output gates, I find it easier to write an expression for the gate's output without the final inversion, with an arrow pointing to just before the inversion bubble. Then, at the wire leading out of the gate (after the bubble), I write the full, complemented expression. This helps ensure I don't forget a complementing bar in the sub-expression, by forcing myself to split the expression-writing task into two steps:

Finally, we write an expression (or pair of expressions) for the last NOR gate:
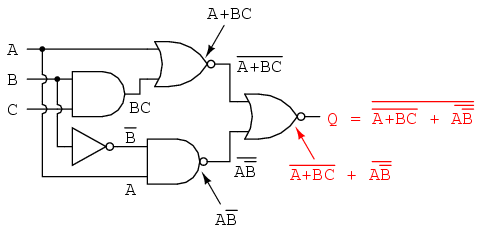
Now, we reduce this expression using the identities, properties, rules, and theorems (DeMorgan's) of Boolean algebra:

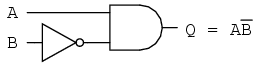
The equivalent gate circuit for this much-simplified expression is as follows:
- REVIEW
- DeMorgan's Theorems describe the equivalence between gates with inverted inputs and gates with inverted outputs. Simply put, a NAND gate is equivalent to a Negative-OR gate, and a NOR gate is equivalent to a Negative-AND gate.
- When "breaking" a complementation bar in a Boolean expression, the operation directly underneath the break (addition or multiplication) reverses, and the broken bar pieces remain over the respective terms.
- It is often easier to approach a problem by breaking the longest (uppermost) bar before breaking any bars under it. You must never attempt to break two bars in one step!
- Complementation bars function as grouping symbols. Therefore, when a bar is broken, the terms underneath it must remain grouped. Parentheses may be placed around these grouped terms as a help to avoid changing precedence.
