Rate-of-change indicator
PARTS AND MATERIALS
- Two 6 volt batteries
- Capacitor, 0.1 µF (Radio Shack catalog # 272-135)
- 1 MΩ resistor
- Potentiometer, single turn, 5 kΩ, linear taper (Radio Shack catalog # 271-1714)
The potentiometer value is not especially critical, although lower-resistance units will, in theory, work better for this experiment than high-resistance units. I've used a 10 kΩ potentiometer for this circuit with excellent results.
CROSS-REFERENCES
Lessons In Electric Circuits, Volume 1, chapter 13: "Capacitors"
LEARNING OBJECTIVES
- How to build a differentiator circuit
- Obtain an empirical understanding of the derivative calculus function
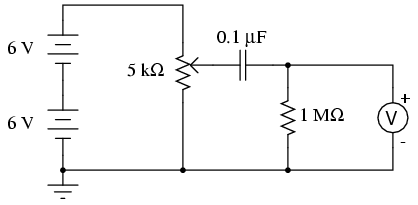
SCHEMATIC DIAGRAM
ILLUSTRATION
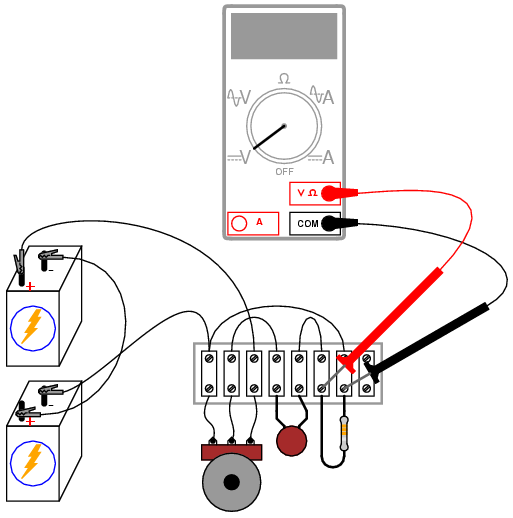
INSTRUCTIONS
Measure voltage between the potentiometer's wiper terminal and the "ground" point shown in the schematic diagram (the negative terminal of the lower 6-volt battery). This is the input voltage for the circuit, and you can see how it smoothly varies between zero and 12 volts as the potentiometer control is turned full-range. Since the potentiometer is used here as a voltage divider, this behavior should be unsurprising to you.
Now, measure voltage across the 1 MΩ resistor while moving the potentiometer control. A digital voltmeter is highly recommended, and I advise setting it to a very sensitive (millivolt) range to obtain the strongest indications. What does the voltmeter indicate while the potentiometer is not being moved? Turn the potentiometer slowly clockwise and note the voltmeter's indication. Turn the potentiometer slowly counter-clockwise and note the voltmeter's indication. What difference do you see between the two different directions of potentiometer control motion?
Try moving the potentiometer in such a way that the voltmeter gives a steady, small indication. What kind of potentiometer motion provides the steadiest voltage across the 1 MΩ resistor?
In calculus, a function representing the rate of change of one variable as compared to another is called the derivative. This simple circuit illustrates the concept of the derivative by producing an output voltage proportional to the input voltage's rate of change over time. Because this circuit performs the calculus function of differentiation with respect to time (outputting the time-derivative of an incoming signal), it is called a differentiator circuit.
Like the averager circuit shown earlier in this chapter, the differentiator circuit is a kind of analog computer. Differentiation is a far more complex mathematical function than averaging, especially when implemented in a digital computer, so this circuit is an excellent demonstration of the elegance of analog circuitry in performing mathematical computations.
More accurate differentiator circuits may be built by combining resistor-capacitor networks with electronic amplifier circuits. For more detail on computational circuitry, go to the "Analog Integrated Circuits" chapter in this Experiments volume.
