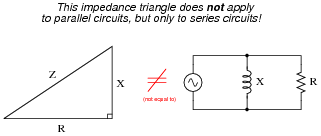Trigonometry for AC circuits
Question 1:
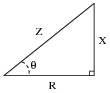
Identify which trigonometric functions (sine, cosine, or tangent) are represented by each of the following ratios, with reference to the angle labeled with the Greek letter "Theta" (
Q):
Reveal Answer

|
|
X
R
|
= tanQ =
|
Opposite
Adjacent
|
|
|
|
|
X
Z
|
= sinQ =
|
Opposite
Hypotenuse
|
|
|
|
|
R
Z
|
= cosQ =
|
Adjacent
Hypotenuse
|
|
|
Notes:
Ask your students to explain what the words "hypotenuse", öpposite", and ädjacent" refer to in a right triangle.
Hide Answer
Question 2:
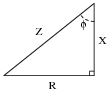
Identify which trigonometric functions (sine, cosine, or tangent) are represented by each of the following ratios, with reference to the angle labeled with the Greek letter "Phi" (
f):
Reveal Answer

|
|
R
X
|
= tanf =
|
Opposite
Adjacent
|
|
|
|
|
X
Z
|
= cosf =
|
Adjacent
Hypotenuse
|
|
|
|
|
R
Z
|
= sinf =
|
Opposite
Hypotenuse
|
|
|
Notes:
Ask your students to explain what the words "hypotenuse", öpposite", and ädjacent" refer to in a right triangle.
Hide Answer
Question 3:
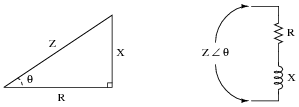
The
impedance triangle is often used to graphically relate Z, R, and X in a series circuit:
Unfortunately, many students do not grasp the significance of this triangle, but rather memorize it as a "trick" used to calculate one of the three variables given the other two. Explain
why a right triangle is an appropriate form to relate these variables, and what each side of the triangle actually represents.
Reveal Answer
Each side of the impedance triangle is actually a
phasor (a vector representing impedance with magnitude and direction):
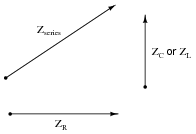
Since the phasor for resistive impedance (Z
R) has an angle of zero degrees and the phasor for reactive impedance (Z
C or Z
L) either has an angle of +90 or -90 degrees, the
phasor sum representing total series impedance will form the hypotenuse of a right triangle when the first to phasors are added (tip-to-tail).
Follow-up question: as a review, explain why resistive impedance phasors always have an angle of zero degrees, and why reactive impedance phasors always have angles of either +90 degrees or -90 degrees.
Notes:
The question is sufficiently open-ended that many students may not realize exactly what is being asked until they read the answer. This is okay, as it is difficult to phrase the question in a more specific manner without giving away the answer!
Hide Answer
Question 4:
Explain why the ïmpedance triangle" is
not proper to use for relating total impedance, resistance, and reactance in parallel circuits as it is for series circuits:
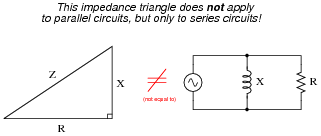
Reveal Answer
Impedances do not add in parallel.
Follow-up question: what kind of a triangle
could be properly applied to a parallel AC circuit, and why?
Notes:
Trying to apply the Z-R-X triangle directly to parallel AC circuits is a common mistake many new students make. Key to knowing when and how to use triangles to graphically depict AC quantities is understanding why the triangle works as an analysis tool and what its sides represent.
Hide Answer
Question 5:
Examine the following circuits, then label the sides of their respective triangles with all the variables that are trigonometrically related in those circuits:
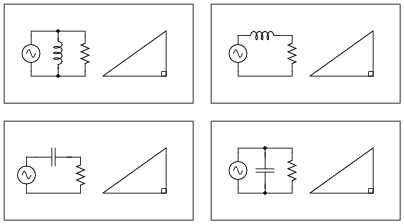
Reveal Answer
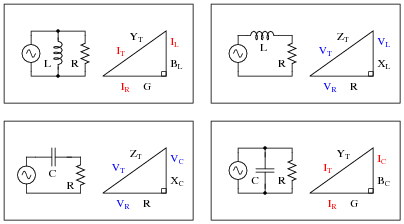
Notes:
This question asks students to identify those variables in each circuit that vectorially add, discriminating them from those variables which do not add. This is extremely important for students to be able to do if they are to successfully apply "the triangle" to the solution of AC circuit problems.
Note that some of these triangles should be drawn upside-down instead of all the same as they are shown in the question, if we are to properly represent the vertical (imaginary) phasor for capacitive impedance and for inductor admittance. However, the point here is simply to get students to recognize what quantities add and what do not. Attention to the direction (up or down) of the triangle's opposite side can come later.
Hide Answer
Question 6:
Use the ïmpedance triangle" to calculate the necessary reactance of this series combination of resistance (R) and inductive reactance (X) to produce the desired total impedance of 145
W:
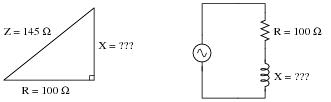
Explain what equation(s) you use to calculate X, and the algebra necessary to achieve this result from a more common formula.
Reveal Answer
X = 105
W, as calculated by an algebraically manipulated version of the Pythagorean Theorem.
Notes:
Be sure to have students show you the form of the Pythagorean Theorem, rather than showing them yourself, since it is so easy for students to research on their own.
Hide Answer
Question 7:
A series AC circuit exhibits a total impedance of 10 k
W, with a phase shift of 65 degrees between voltage and current. Drawn in an impedance triangle, it looks like this:
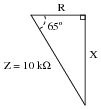
We know that the
sine function relates the sides X and Z of this impedance triangle with the 65 degree angle, because the sine of an angle is the ratio of
opposite to
hypotenuse, with X being opposite the 65 degree angle. Therefore, we know we can set up the following equation relating these quantities together:
Solve this equation for the value of X, in ohms.
Reveal Answer
X = 9.063 k
W
Notes:
Ask your students to show you their algebraic manipulation(s) in setting up the equation for evaluation.
Hide Answer
Question 8:
A series AC circuit exhibits a total impedance of 2.5 k
W, with a phase shift of 30 degrees between voltage and current. Drawn in an impedance triangle, it looks like this:
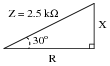
Use the appropriate trigonometric functions to calculate the equivalent values of R and X in this series circuit.
Reveal Answer
R = 2.165 k
W
X = 1.25 k
W
Notes:
There are a few different ways one could solve for R and X in this trigonometry problem. This would be a good opportunity to have your students present problem-solving strategies on the board in front of class so everyone gets an opportunity to see multiple techniques.
Hide Answer
Question 9:
A parallel AC circuit draws 8 amps of current through a purely resistive branch and 14 amps of current through a purely inductive branch:
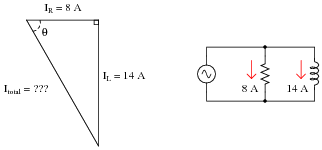
Calculate the total current and the angle
Q of the total current, explaining your trigonometric method(s) of solution.
Reveal Answer
I
total = 16.12 amps
Q = 60.26
o (negative, if you wish to represent the angle according to the standard coordinate system for phasors).
Follow-up question: in calculating
Q, it is recommended to use the arctangent function instead of either the arcsine or arc-cosine functions. The reason for doing this is accuracy: less possibility of compounded error, due to either rounding and/or calculator-related (keystroke) errors. Explain why the use of the arctangent function to calculate
Q incurs less chance of error than either of the other two arcfunctions.
Notes:
The follow-up question illustrates an important principle in many different disciplines: avoidance of unnecessary risk by choosing calculation techniques using given quantities instead of derived quantities. This is a good topic to discuss with your students, so make sure you do so.
Hide Answer
Question 10:
A parallel RC circuit has 10
mS of susceptance (B). How much conductance (G) is necessary to give the circuit a (total) phase angle of 22 degrees?

Reveal Answer
G = 24.75
mS
Follow-up question: how much resistance is this, in ohms?
Notes:
Ask your students to explain their method(s) of solution, including any ways to double-check the correctness of the answer.
Hide Answer
Question 11:
The
Pythagorean Theorem is used to calculate the length of the hypotenuse of a right triangle given the lengths of the other two sides:
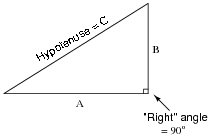
Write the standard form of the Pythagorean Theorem, and give an example of its use.
Reveal Answer
I'll let you research this one on your own!
Follow-up question: identify an application in AC circuit analysis where the Pythagorean Theorem would be useful for calculating a circuit quantity such as voltage or current.
Notes:
The Pythagorean Theorem is easy enough for students to find on their own that you should not need to show them. A memorable illustration of this theorem are the side lengths of a so-called 3-4-5 triangle. Don't be surprised if this is the example many students choose to give.
Hide Answer
Question 12:
Use the ïmpedance triangle" to calculate the impedance of this series combination of resistance (R) and inductive reactance (X):
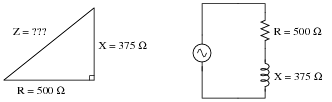
Explain what equation(s) you use to calculate Z.
Reveal Answer
Z = 625
W, as calculated by the Pythagorean Theorem.
Notes:
Be sure to have students show you the form of the Pythagorean Theorem, rather than showing them yourself, since it is so easy for students to research on their own.
Hide Answer
Question 13:
Trigonometric functions such as
sine,
cosine, and
tangent are useful for determining the ratio of right-triangle side lengths given the value of an angle. However, they are not very useful for doing the reverse: calculating an angle given the lengths of two sides.
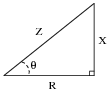
Suppose we wished to know the value of angle
Q, and we happened to know the values of Z and R in this impedance triangle. We could write the following equation, but in its present form we could not solve for
Q:
The only way we can algebraically isolate the angle
Q in this equation is if we have some way to ündo" the cosine function. Once we know what function will ündo" cosine, we can apply it to both sides of the equation and have
Q by itself on the left-hand side.
There is a class of trigonometric functions known as
inverse or
ärc" functions which will do just that: ündo" a regular trigonometric function so as to leave the angle by itself. Explain how we could apply an ärc-function" to the equation shown above to isolate
Q.
Reveal Answer
|
cosQ =
|
R
Z
|
Original equation |
|
|
. . . applying the ärc-cosine" function to both sides . . . |
|
|
arccos( cosQ) = arccos
|
�
�
|
R
Z
|
�
�
|
|
|
Notes:
I like to show the purpose of trigonometric arcfunctions in this manner, using the cardinal rule of algebraic manipulation (do the same thing to both sides of an equation) that students are familiar with by now. This helps eliminate the mystery of arcfunctions for students new to trigonometry.
Hide Answer
Question 14:
A series AC circuit contains 1125 ohms of resistance and 1500 ohms of reactance for a total circuit impedance of 1875 ohms. This may be represented graphically in the form of an impedance triangle:
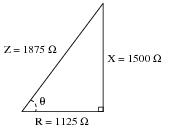
Since all side lengths on this triangle are known, there is no need to apply the Pythagorean Theorem. However, we may still calculate the two non-perpendicular angles in this triangle using ïnverse" trigonometric functions, which are sometimes called
arcfunctions.
Identify which arc-function should be used to calculate the angle
Q given the following pairs of sides:
Show how three different trigonometric arcfunctions may be used to calculate the same angle
Q.
Reveal Answer
Challenge question: identify three
more arcfunctions which could be used to calculate the same angle
Q.
Notes:
Some hand calculators identify arc-trig functions by the letter Ä" prepending each trigonometric abbreviation (e.g. ÄSIN" or ÄTAN"). Other hand calculators use the inverse function notation of a -1 exponent, which is not actually an exponent at all (e.g. sin-1 or tan-1). Be sure to discuss function notation on your students' calculators, so they know what to invoke when solving problems such as this.
Hide Answer
Question 15:
Students studying AC electrical theory become familiar with the
impedance triangle very soon in their studies:
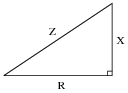
What these students might not ordinarily discover is that this triangle is also useful for calculating electrical quantities other than impedance. The purpose of this question is to get you to discover some of the triangle's other uses.
Fundamentally, this right triangle represents
phasor addition, where two electrical quantities at right angles to each other (resistive versus reactive) are added together. In series AC circuits, it makes sense to use the impedance triangle to represent how resistance (R) and reactance (X) combine to form a total impedance (Z), since resistance and reactance are special forms of impedance themselves, and we know that impedances
add in series.
List all of the electrical quantities you can think of that add (in series or in parallel) and then show how similar triangles may be drawn to relate those quantities together in AC circuits.
Reveal Answer
Electrical quantities that add:
-
�
-
Series impedances
-
�
- Series voltages
-
�
- Parallel admittances
-
�
- Parallel currents
-
�
- Power dissipations
I will show you one graphical example of how a triangle may relate to electrical quantities other than series impedances:
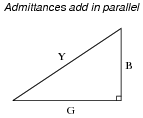
Notes:
It is very important for students to understand that the triangle only works as an analysis tool when applied to quantities that add. Many times I have seen students try to apply the Z-R-X impedance triangle to parallel circuits and fail because parallel impedances do not add. The purpose of this question is to force students to think about where the triangle is applicable to AC circuit analysis, and not just to use it blindly.
The power triangle is an interesting application of trigonometry applied to electric circuits. You may not want to discuss power with your students in great detail if they are just beginning to study voltage and current in AC circuits, because power is a sufficiently confusing subject on its own.
Hide Answer
Question 16:
The
Pythagorean Theorem is used to calculate the length of the hypotenuse of a right triangle given the lengths of the other two sides:
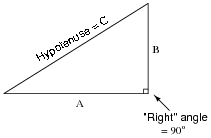
Manipulate the standard form of the Pythagorean Theorem to produce a version that solves for the length of A given B and C, and also write a version of the equation that solves for the length of B given A and C.
Reveal Answer
Standard form of the Pythagorean Theorem:
Solving for A:
Solving for B:
Notes:
The Pythagorean Theorem is easy enough for students to find on their own that you should not need to show them. A memorable illustration of this theorem are the side lengths of a so-called 3-4-5 triangle. Don't be surprised if this is the example many students choose to give.
Hide Answer
Question 17:
A rectangular building foundation with an area of 18,500 square feet measures 100 feet along one side. You need to lay in a diagonal run of conduit from one corner of the foundation to the other. Calculate how much conduit you will need to make the run:
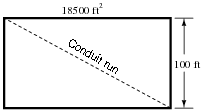
Also, write an equation for calculating this conduit run length (L) given the rectangular area (A) and the length of one side (x).
Reveal Answer
Conduit run = 210 feet, 3.6 inches from corner to corner.
Note: the following equation is not the only form possible for calculating the diagonal length. Do not be worried if your equation does not look exactly like this!
Notes:
Determining the necessary length of conduit for this question involves both the Pythagorean theorem and simple geometry.
Most students will probably arrive at this form for their diagonal length equation:
While this is perfectly correct, it is an interesting exercise to have students convert the equation from this (simple) form to that given in the answer. It is also a very practical question, as equations given in reference books do not always follow the most direct form, but rather are often written in such a way as to look more esthetically pleasing. The simple and direct form of the equation shown here (in the Notes section) looks ügly" due to the fraction inside the radicand.
Hide Answer
Question 18:
Evaluate the length of side x in this right triangle, given the lengths of the other two sides:
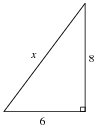
Reveal Answer
x = 10
Notes:
This question is a straight-forward test of students' ability to identify and apply the 3-4-5 ratio to a right triangle.
Hide Answer
Question 19:
Evaluate the length of side x in this right triangle, given the lengths of the other two sides:
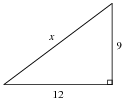
Reveal Answer
x = 15
Notes:
This question is a straight-forward test of students' ability to identify and apply the 3-4-5 ratio to a right triangle.
Hide Answer
Question 20:
Use a triangle to calculate the total voltage of the source for this series RC circuit, given the voltage drop across each component:
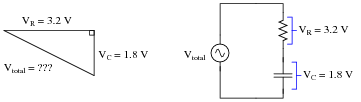
Explain what equation(s) you use to calculate V
total, as well as why we must geometrically add these voltages together.
Reveal Answer
V
total = 3.672 volts, as calculated by the Pythagorean Theorem
Notes:
Be sure to have students show you the form of the Pythagorean Theorem, rather than showing them yourself, since it is so easy for students to research on their own.
Hide Answer
Question 21:
Use the ïmpedance triangle" to calculate the necessary resistance of this series combination of resistance (R) and inductive reactance (X) to produce the desired total impedance of 5.2 k
W:
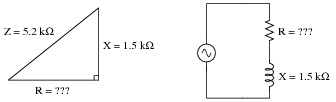
Explain what equation(s) you use to calculate R, and the algebra necessary to achieve this result from a more common formula.
Reveal Answer
R = 4.979 k
W, as calculated by an algebraically manipulated version of the Pythagorean Theorem.
Notes:
Be sure to have students show you the form of the Pythagorean Theorem, rather than showing them yourself, since it is so easy for students to research on their own.
Hide Answer
Question 22:
Use the ïmpedance triangle" to calculate the necessary reactance of this series combination of resistance (R) and capacitive reactance (X) to produce the desired total impedance of 300
W:
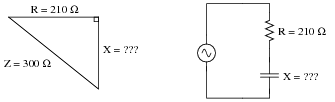
Explain what equation(s) you use to calculate X, and the algebra necessary to achieve this result from a more common formula.
Reveal Answer
X = 214.2
W, as calculated by an algebraically manipulated version of the Pythagorean Theorem.
Notes:
Be sure to have students show you the form of the Pythagorean Theorem, rather than showing them yourself, since it is so easy for students to research on their own.
Hide Answer
Question 23:
A parallel AC circuit draws 100 mA of current through a purely resistive branch and 85 mA of current through a purely capacitive branch:
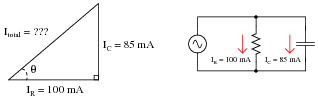
Calculate the total current and the angle
Q of the total current, explaining your trigonometric method(s) of solution.
Reveal Answer
I
total = 131.2 mA
Q = 40.36
o
Follow-up question: in calculating
Q, it is recommended to use the arctangent function instead of either the arcsine or arc-cosine functions. The reason for doing this is accuracy: less possibility of compounded error, due to either rounding and/or calculator-related (keystroke) errors. Explain why the use of the arctangent function to calculate
Q incurs less chance of error than either of the other two arcfunctions.
Notes:
The follow-up question illustrates an important principle in many different disciplines: avoidance of unnecessary risk by choosing calculation techniques using given quantities instead of derived quantities. This is a good topic to discuss with your students, so make sure you do so.
Hide Answer