Active loads in amplifier circuits
Question 1:
We know that the current in a series circuit may be calculated with this formula:
|
We also know that the voltage dropped across any single resistor in a series circuit may be calculated with this formula:
|
Combine these two formulae into one, in such a way that the I variable is eliminated, leaving only ER expressed in terms of Etotal, Rtotal, and R.
|
Follow-up question: algebraically manipulate this equation to solve for Etotal in terms of all the other variables. In other words, show how you could calculate for the amount of total voltage necessary to produce a specified voltage drop (ER) across a specified resistor (R), given the total circuit resistance (Rtotal).
Notes:
Though this "voltage divider formula" may be found in any number of electronics reference books, your students need to understand how to algebraically manipulate the given formulae to arrive at this one.
Question 2:
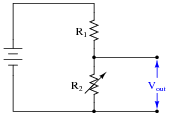
Determine what will happen to the output voltage (Vout) and resistor R1's current (IR1) in this circuit as the resistance of R2 is increased:
|
|
Notes:
Nothing special here - just a qualitative analysis of a very simple voltage divider circuit.
Question 3:
Suppose we were to compare the performance of two voltage divider circuits side-by-side. The circuit on the left has one variable resistor (R2), while the circuit on the right has two variable resistors (R1 and R2). The right-hand circuit's resistors are ganged together in such a way that as one resistance increases, the other will decrease by the same amount, keeping the circuit's total resistance constant:

|
|
Knowing that the voltage output by a voltage divider is described by the following formula, determine which voltage divider circuit yields the greatest change in output voltage for a given change in R2's resistance.
|
Follow-up question #1: what happens to the amount of current in each circuit for a given change in R2 resistance? Explain why.
Follow-up question #2: explain how a potentiometer performs the exact function as the second circuit with the two (complementarily) ganged rheostats.
Notes:
Understanding the mathematical basis for the answer may be a significant leap for some students. If they experience trouble understanding how the voltage divider formula proves the answer, have them try a "thought experiment" with really simple numbers:
- �
- Initial conditions:
- R1 = 1 W
- R2 = 1 W
- Vbattery = 1 volt
Now, increase R2 from 1 W to 2 W and see which voltage divider circuit has experienced the greatest change in output voltage. Once these example quantities are placed into the respective formulae, it should become easy to see how the voltage divider formula explains the larger voltage swing of the second divider circuit.
Point out to your students that this is an example of practical problem-solving: performing a "thought experiment" with really simple quantities to numerically explore how two different systems react to change. Although there is nothing particularly difficult about this technique, many students avoid it because they think there must be some easier way (a ready-made explanation, as opposed to a thought experiment of their own) to understand the concept. Getting students over this attitude barrier is a difficult yet crucial step in them developing self-teaching ability.
Question 4:
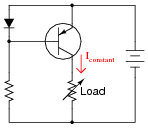
The purpose of a current mirror circuit is to maintain constant current through a load despite changes in that load's resistance:
|
|
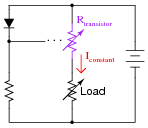
If we were to crudely model the transistor's behavior as an automatically-varied rheostat - constantly adjusting resistance as necessary to keep load current constant - how would you describe this rheostat's response to changes in load resistance?
|
|
In other words, as Rload increases, what does Rtransistor do - increase resistance, decrease resistance, or remain the same resistance it was before? How does the changing value of Rtransistor affect total circuit resistance?
Notes:
This model of current mirror transistor behavior, albeit crude, serves as a good introduction to the subject of active loads in transistor amplifier circuits. This is where a transistor is configured to operate as a constant-current regulator, then placed in series with an amplifying transistor to yield much greater voltage gains than what is possible with a passive (fixed resistor) load.
Question 5:
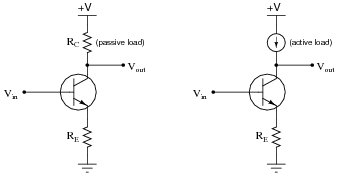
An interesting technique to achieve extremely high voltage gain from a single-stage transistor amplifier is to substitute an active load for the customary load resistor (located at the collector terminal):
|
|
Usually, this äctive load" takes the form of a current mirror circuit, behaving as a current regulator rather than as a true current source.
Explain why the presence of an active load results in significantly more voltage gain than a plain (passive) resistor. If the active load were a perfect current regulator, holding collector current absolutely constant despite any change in collector-base conductivity for the main amplifying transistor, what would the voltage gain be?
Notes:
There is more than one way to comprehend this effect, and why it works as it does. One of the more sophisticated ways is to consider what the internal resistance of a perfect current source is: infinite. Ask your students how they contemplated this effect, and what means they employed to grasp the concept.
Question 6:
Identify as many active loads as you can in the following (simplified) schematic of an LM324 operational amplifier circuit:
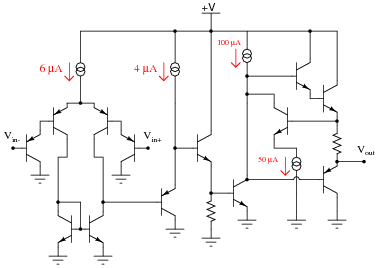
|
|
Notes:
Even if students do not yet know what an öperational amplifier" circuit is, they should still be able to identify transistor stages, configurations, and active loads. In this case, most of the active loads are obvious (as revealed by the current source symbols).
Don't be surprised if some of your students point out that the differential pair in this opamp circuit looks üpside-down" compared to what they've seen before for differential pair circuits. Let them know that this is not really an issue, and that the differential pair works the same in this configuration.
Question 7:
Identify as many active loads as you can in the following schematic of an LM741 operational amplifier circuit,along with their respective (amplifying) transistors:
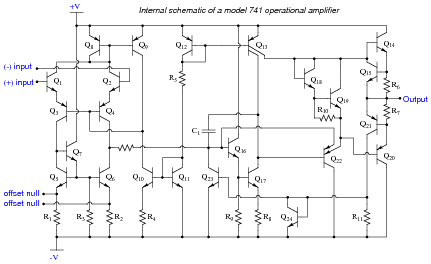
|
|
- �
- Q6 is an active load for Q4
- �
- Q23 is an active load for Q4
- �
- Q13 is an active load for Q17 and Q22
Notes:
Even if students do not yet know what an öperational amplifier" circuit is, they should still be able to identify transistor stages, configurations, and active loads.
