Algebraic equation manipulation for electric circuits
Question 1:
The electrical resistance of a conductor at any temperature may be calculated by the following equation:
Where,
R
T = Resistance of conductor at temperature T
R
r = Resistance of conductor at reference temperature T
r
a = Temperature coefficient of resistance at reference temperature T
r
Simplify this equation by means of factoring.
Reveal Answer
Follow-up question: when plotted on a graph with temperature (T) as the independent variable and resistance (R
T) as the dependent variable (i.e. a two-axis graph with T on the horizontal and R on the vertical), is the resulting plot linear? Why or why not? How is it possible to tell just by looking at the equation, prior to actually plotting on a graph?
Notes:
Just an exercise in algebra here!
Hide Answer
Question 2:
The equation for voltage gain (A
V) in a typical noninverting, single-ended opamp circuit is as follows:
Where,
R
1 is the feedback resistor (connecting the output to the inverting input)
R
2 is the other resistor (connecting the inverting input to ground)
Suppose we wished to change the voltage gain in the following circuit from 5 to 6.8, but only had the freedom to alter the resistance of R
2:
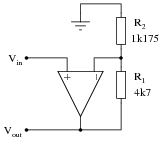
Algebraically manipulate the gain equation to solve for R
2, then determine the necessary value of R
2 in this circuit to give it a voltage gain of 6.8.
Reveal Answer
For the circuit shown, R
2 would have to be set equal to 810.3
W.
Notes:
Nothing more than a little algebra to obtain the answers for this question!
Hide Answer
Question 3:
The equation for voltage gain (A
V) in a typical inverting, single-ended opamp circuit is as follows:
Where,
R
1 is the feedback resistor (connecting the output to the inverting input)
R
2 is the other resistor (connecting the inverting input to voltage signal input terminal)
Suppose we wished to change the voltage gain in the following circuit from 3.5 to 4.9, but only had the freedom to alter the resistance of R
2:
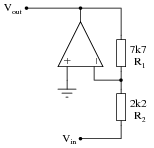
Algebraically manipulate the gain equation to solve for R
2, then determine the necessary value of R
2 in this circuit to give it a voltage gain of 4.9.
Reveal Answer
For the circuit shown, R
2 would have to be set equal to 1.571 k
W.
Notes:
Nothing more than a little algebra to obtain the answers for this question!
Hide Answer
Question 4:
The following equations solve for the output voltage of various switching converter circuits (unloaded), given the switch duty cycle D and the input voltage:
|
Vout = D Vin (Buck converter circuit) |
|
|
Vout =
|
Vin
1 - D
|
(Boost converter circuit) |
|
|
Vout =
|
D Vin
1 - D
|
(Inverting or Cuk converter circuit) |
|
Manipulate each of these equations to solve for duty cycle (D) in terms of the input voltage (V
in) and desired output voltage (V
out). Remember that duty cycle is always a quantity between 0 and 1, inclusive.
Reveal Answer
|
D =
|
Vout
Vin
|
(Buck converter circuit) |
|
|
D = 1 - |
�
�
|
Vin
Vout
|
�
�
|
(Boost converter circuit) |
|
|
D =
|
Vout
Vin + Vout
|
(Inverting or Cuk converter circuit) |
|
Notes:
Given the equations for these converter circuit types solving for output voltage in terms of input voltage and duty cycle D, this question is nothing more than an exercise in algebraic manipulation.
Note to your students that all of these equations assume a condition of zero load on the converter circuit. When loads are present, of course, the output voltage will not be the same as what is predicted by these neat, simple formulae. Although these DC-DC power converter circuits are commonly referred to as "regulators," it is somewhat misleading to do so because it falsely implies a capacity for self-correction of output voltage. Only when coupled to a feedback control network are any of these converter circuits capable of actually regulating output voltage to a set value.
Hide Answer
Question 5:
Solve for n in the following equations:
Equation 1:
-56 =
-14n
Equation 2: 54
- n = 10
Equation 3:
4/
n = 12
Equation 4: 28 = 2
- n
Reveal Answer
Equation 1: n = 4
Equation 2: n = 44
Equation 3: n = 0.[
`333]
Equation 4: n =
-26
Notes:
Have your students come to the front of the class and show everyone else the techniques they used to solve for the value of a in each equation. Remind them to document each and every step in the process, so that nothing is left to guess or to chance.
Equations 2 through 4 require two steps to solve for n. Equation 1 only requires a single step, but the two negative numbers may be a bit confusing to some.
Hide Answer
Question 6:
The formula for calculating total resistance of three series-connected resistors is as follows:
Algebraically manipulate this equation to solve for one of the series resistances (R
1) in terms of the other two series resistances (R
2 and R
3) and the total resistance (R). In other words, write a formula that solves for R
1 in terms of all the other variables.
Reveal Answer
|
R1 = R - (R2 + R3) or R1 = R - R2 - R3 |
|
Notes:
This question is nothing more than practice algebraically manipulating equations. Ask your students to show you how they solved it, and how the two given answers are equivalent.
Hide Answer
Question 7:
Manipulate this equation to solve for resistor value R
1, given the values of R
2 and R
parallel:
|
Rparallel =
|
R1 R2
R1 + R2
|
|
|
Then, give an example of a practical situation where you might use this new equation.
Reveal Answer
|
R1 =
|
R2 Rparallel
R2 - Rparallel
|
|
|
I'll let you figure out a situation where this equation would be useful!
Notes:
This question is really nothing more than an exercise in algebraic manipulation.
Hide Answer
Question 8:
The formula for calculating total resistance of three parallel-connected resistors is as follows:
Algebraically manipulate this equation to solve for one of the parallel resistances (R
1) in terms of the other two parallel resistances (R
2 and R
3) and the total resistance (R). In other words, write a formula that solves for R
1 in terms of all the other variables.
Reveal Answer
Notes:
This question is nothing more than practice algebraically manipulating equations. Ask your students to show you how they solved it, and how the two given answers are equivalent.
Hide Answer
Question 9:
The power dissipation of a transistor is given by the following equation:
Manipulate this equation to solve for beta, given all the other variables.
Reveal Answer
Notes:
Although this question is essentially nothing more than an exercise in algebraic manipulation, it is also a good lead-in to a discussion on the importance of power dissipation as a semiconductor device rating.
High temperature is the bane of most semiconductors, and high temperature is caused by excessive power dissipation. A classic example of this, though a bit dated, is the temperature sensitivity of the original germanium transistors. These devices were extremely sensitive to heat, and would fail rather quickly if allowed to overheat. Solid state design engineers had to be very careful in the techniques they used for transistor circuits to ensure their sensitive germanium transistors would not suffer from "thermal runaway" and destroy themselves.
Silicon is much more forgiving then germanium, but heat is still a problem with these devices. At the time of this writing (2004), there is promising developmental work on silicon carbide and gallium nitride transistor technology, which is able to function under much higher temperatures than silicon.
Hide Answer
Question 10:
The decay of a variable over time in an RC or LR circuit follows this mathematical expression:
Where,
e = Euler's constant (
� 2.718281828)
t = Time, in seconds
t = Time constant of circuit, in seconds
For example, if we were to evaluate this expression and arrive at a value of 0.398, we would know the variable in question has decayed from 100% to 39.8% over the period of time specified.
However, calculating the amount of time it takes for a decaying variable to reach a specified percentage is more difficult. We would have to manipulate the equation to solve for t, which is part of an exponent.
Show how the following equation could be algebraically manipulated to solve for t, where x is the number between 0 and 1 (inclusive) representing the percentage of original value for the variable in question:
Note: the "trick" here is how to isolate the exponent [(
-t)/(
t)]. You will have to use the natural logarithm function!
Reveal Answer
Showing all the necessary steps:
Notes:
In my experience, most American high school graduates are extremely weak in logarithms. Apparently this is not taught very well at the high school level, which is a shame because logarithms are a powerful mathematical tool. You may find it necessary to explain to your students what a logarithm is, and exactly why it ün-does" the exponent.
When forced to give a quick presentation on logarithms, I usually start with a generic definition:
|
Logarithm defined: logb c = a
|
|
Verbally defined, the logarithm function asks us to find the power (a) of the base (b) that will yield c.
Next, I introduce the common logarithm. This, of course, is a logarithm with a base of 10. A few quick calculator exercises help students grasp what the common logarithm function is all about:
After this, I introduce the
natural logarithm: a logarithm with a base of e (Euler's constant):
|
Natural logarithm defined: lnx = loge x
|
|
Have your students do this simple calculation on their calculators, and explain the result:
Next comes an exercise to help them understand how logarithms can ündo" exponentiation. Have your students calculate the following values:
Now, have them take the natural logarithms of each of those answers. They will find that they arrive at the original exponent values (2, 3, and 4, respectively). Write this relationship on the board as such for your students to view:
Ask your students to express this relationship in general form, using the variable x for the power instead of an actual number:
It should now be apparent that the natural logarithm function has the ability to ündo" a power of e. Now it should be clear to your students why the given sequence of algebraic manipulations in the answer for this question is true.
Hide Answer
Question 11:
Voltage and current gains, expressed in units of decibels, may be calculated as such:
|
AV(dB) = 10 log( AV(ratio) ) 2 |
|
|
AI(dB) = 10 log( AI(ratio) ) 2 |
|
Another way of writing this equation is like this:
What law of algebra allows us to simplify a logarithmic equation in this manner?
Reveal Answer
Challenge question: knowing this algebraic law, solve for x in the following equation:
Notes:
Logarithms are a confusing, but powerful, algebraic tool. In this example, we see how the logarithm of a power function is converted into a simple multiplication function.
The challenge question asks students to apply this relationship to an equation not containing logarithms at all. However, the fundamental rule of algebra is that you may perform any operation (including logarithms) to any equation so long as you apply it equally to both sides of the equation. Logarithms allow us to take an algebra problem such as this and simplify it significantly.
Hide Answer
Question 12:
Solve for the value of x in the following equations:
Reveal Answer
Notes:
Have your students come to the front of the class and show everyone else the techniques they used to solve for the value of x in each equation. Remind them to document each and every step in the process, so that nothing is left to guess or to chance.
Hide Answer
Question 13:
Solve for the value of x in the following equations:
Reveal Answer
Notes:
Have your students come to the front of the class and show everyone else the techniques they used to solve for the value of x in each equation. Remind them to document each and every step in the process, so that nothing is left to guess or to chance.
Hide Answer
Question 14:
Solve for the value of a in the following equations:
Equation 1: a
- 4 = 10
Equation 2: 30 = a + 3
Equation 3:
-2a = 9
Equation 4:
a/
4 = 3.5
Reveal Answer
Equation 1: a = 14
Equation 2: a = 27
Equation 3: a =
-4.5
Equation 4: a = 14
Notes:
Have your students come to the front of the class and show everyone else the techniques they used to solve for the value of a in each equation. Remind them to document each and every step in the process, so that nothing is left to guess or to chance.
Hide Answer
Question 15:
Solve for the value of x in the following equations:
Reveal Answer
Notes:
Have your students come to the front of the class and show everyone else the techniques they used to solve for the value of x in each equation. Remind them to document each and every step in the process, so that nothing is left to guess or to chance.
Hide Answer
Question 16:
Solve for the value of x in the following equations:
Reveal Answer
Notes:
Have your students come to the front of the class and show everyone else the techniques they used to solve for the value of x in each equation. Remind them to document each and every step in the process, so that nothing is left to guess or to chance.
Hide Answer
Question 17:
Manipulate each of these equations to solve for a:
|
|
b - a
c
|
= d
|
�
|
a + b
|
= c2 d
|
|
Reveal Answer
Notes:
Have your students come to the front of the class and show everyone else the techniques they used to solve for a in each equation. Remind them to document each and every step in the process, so that nothing is left to guess or to chance.
Hide Answer
Question 18:
Manipulate each of these equations to solve for a:
|
|
a - b
c
|
= d2 b + a2 =
|
c
d
|
|
|
Reveal Answer
Notes:
Have your students come to the front of the class and show everyone else the techniques they used to solve for a in each equation. Remind them to document each and every step in the process, so that nothing is left to guess or to chance.
Hide Answer
Question 19:
Calculate all currents in this DC circuit:
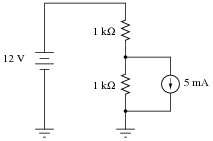
Hint: it may help you to set up the necessary equation by labeling the current through the lower resistor as I and the current through the upper resistor as I + 0.005.
Reveal Answer
Upper resistor current = 8.5 mA; lower resistor current = 3.5 mA
Notes:
This is an interesting circuit to mathematically analyze. While not requiring simultaneous equations, or even a network theorem such as Superposition or Thévenin's, it is nevertheless a good exercise in applying the basic laws of circuit analysis (Ohm's, Kirchhoff's) and algebra.
Hide Answer



