Binary math
Question 1:
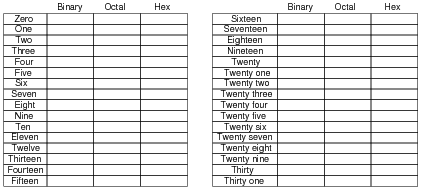
Counting practice: count from zero to thirty-one in binary, octal, and hexadecimal:
|
|
Notes:
In order to familiarize students with these ßtrange" numeration systems, I like to begin each day of digital circuit instruction with counting practice. Students need to be fluent in these numeration systems by the time they are finished studying digital circuits!
One suggestion I give to students to help them see patterns in the count sequences is "pad" the numbers with leading zeroes so that all numbers have the same number of characters. For example, instead of writing "10" for the binary number two, write "00010". This way, the patterns of character cycling (especially binary, where each successively higher-valued bit has half the frequency of the one before it) become more evident to see.
Question 2:
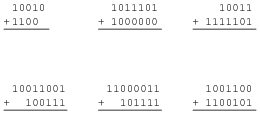
Add the following binary numbers:
|
|

|
|
Notes:
Ask your students to describe what differences exist between manually adding binary numbers and manually adding decimal numbers, if any.
Question 3:
If the numbers sixteen and nine are added in binary form, will the answer be any different than if the same quantities are added in decimal form? Explain.
Notes:
Although this may seem like a trivial question, I've met electronics technicians who actually believed that the form of numeration affected the outcome of certain mathematical operations. In particular, I met one fellow who believed the number p was fundamentally different in binary form than it was in decimal form: that a binary "pi" was not the same quantity as a decimal "pi". I challenged his belief by applying some Socratic irony:
- Me: How do you use a hand calculator to determine the circumference of a circle, given its diameter? For example, a circle with a diameter of 5 feet has a circumference of . . .
Him: By multiplying the diameter times "pi". 5 feet times "pi" is a little over 15 feet.
Me: Does a calculator give you the correct answer?
Him: Of course it does.
Me: Does an electronic calculator use decimal numbers, internally, to do math?
Him: No, it uses binary numbers, because its circuitry is made up of logic gates . . . (long pause) . . . Oh, now I see! If the type of number system mattered in doing math, digital computers and calculators would arrive at different answers for arithmetic problems than we would doing the math by hand!
Question 4:
What is the one's complement of a binary number? If you had to describe this principle to someone who just learned what binary numbers are, what would you say?
Determine the one's complement for the following binary numbers:
- �
- 100010102
- �
- 110101112
- �
- 111100112
- �
- 111111112
- �
- 111112
- �
- 000000002
- �
- 000002
- �
- 100010102: One's complement = 011101012
- �
- 110101112: One's complement = 001010002
- �
- 111100112: One's complement = 000011002
- �
- 111111112: One's complement = 000000002
- �
- 111112: One's complement = 000002
- �
- 000000002: One's complement = 111111112
- �
- 000002: One's complement = 111112
Follow-up question: is the one's complement 111111112 identical to the one's complement of 111112? How about the one's complements of 000000002 and 000002? Explain.
Notes:
The principle of a öne's complement" is very, very simple. Don't give your students any hints at all concerning the technique for finding a one's complement. Rather, let them research it and present it to you on their own!
Be sure to discuss the follow-up question, concerning the one's complement of different-width binary numbers. There is a very important lesson to be learned here!
Question 5:
Determine the two's complement of the binary number 011001012. Explain how you did the conversion, step by step.
Next, determine the two's complement representation of the quantity five for a digital system where all numbers are represented by four bits, and also for a digital system where all numbers are represented by eight bits (one byte). Identify the difference that "word length" (the number of bits allocated to represent quantities in a particular digital system) makes in determining the two's complement of any number.
The two's complement of five is 1011 in the four-bit system. It is 11111011 in the eight-bit system.
Notes:
The point about word-length is extremely important. One cannot arrive at a definite two's complement for any number unless the word length is first known!
Question 6:
In a computer system that represents all integer quantities using two's complement form, the most significant bit has a negative place-weight. For an eight-bit system, the place weights are as follows:
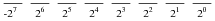
|
|
Given this place-weighting, convert the following eight-bit two's complement binary numbers into decimal form:
- �
- 010001012 =
- �
- 011100002 =
- �
- 110000012 =
- �
- 100101112 =
- �
- 010101012 =
- �
- 101010102 =
- �
- 011001012 =
- �
- 010001012 = 6910
- �
- 011100002 = 11210
- �
- 110000012 = -6310
- �
- 100101112 = -10510
- �
- 010101012 = 8510
- �
- 101010102 = -8610
- �
- 011001012 = 10110
Notes:
Students accustomed to checking their conversions with calculators may find difficulty with these examples, given the negative place weight! Two's complement notation may seem unusual at first, but it possesses decided advantages in binary arithmetic.
Question 7:
In an eight-bit digital system, where all numbers are represented in two's complement form, what is the largest (most positive) quantity that may be represented with those eight bits? What is the smallest (most negative) quantity that may be represented? Express your answers in both binary (two's complement) and decimal form.
Smallest (most negative): 100000002 = -12810
Notes:
The most important concept in this question is that of range: what are the limits of the representable quantities, given a certain number of bits. Two's complement just makes the concept a bit more interesting.
Question 8:
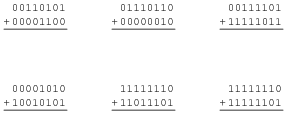
Two's complement notation really shows its value in binary addition, where positive and negative quantities may be handled with equal ease. Add the following byte-long (8 bit) two's complement numbers together, and then convert all binary quantities into decimal form to verify the accuracy of the addition:
|
|

|
|
Notes:
Have your students do some of these problems on the board, in front of class for all to see. Ask students what happens to the left-most "carry" bit, if it exists in any of these problems. Ask them why we do what we do with that bit, when we would usually place it in our answer.
Question 9:
Add the following eight-bit two's complement numbers together, and then convert all binary quantities into decimal form to verify the accuracy of the addition:

|
|

|
|
Follow-up question: Why are some of these answers incorrect? Hint: perform the additions in decimal form rather than binary form, and then explain why those answers are not represented in the binary answers.
Notes:
This question introduces students to the phenomenon of overflow. This is a very important principle to understand, because real computer systems must deal with this condition properly, so as not to output incorrect answers!
Question 10:
How is it possible to tell that overflow has occurred in the addition of binary numbers, without converting the binary sums to decimal form and having a human being verify the answers?
Challenge question: under what condition(s) is overflow impossible? When can we add two binary numbers together and know with certainty that the answer will be correct?
Notes:
Later, this concept of overflow checking should be applied to a real circuit, with students designing logic gate arrays to detect the presence of overflow. First, though, they must learn to recognize its presence analytically.
Question 11:
What is a floating-point number in a digital system?
Notes:
Ask your students why computer systems would have need for floating point numbers. What's wrong with the standard forms of binary numbers that we've explored thus far?
