Capacitance
Question 1:
Write an equation describing the precise mathematical relationship between electric charge (Q), capacitance (C), and voltage (V).
Follow-up question: calculate the amount of charge stored in a 330 mF capacitor charged with a voltage of 12 volts.
Notes:
This is one of those equations usually discussed somewhere in the first few months of basic electronics education, and promptly forgotten by most. It can be very useful, however, when dealing with charge pumps and other switched-capacitor circuitry.
Question 2:
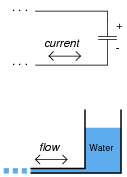
How does the rate of charge flow (current) into and out of a capacitor relate to the amount of voltage across its terminals? How does the rate of water flow into and out of a vessel relate to the amount of water stored in that vessel?
|
|
Notes:
The existence of such an appropriate analogy for capacitor action makes an explanation unnecessary, even if the concept takes a bit of thought to comprehend at first. It is important that students clearly distinguish the quantities of current, voltage, and charge in a capacitor circuit just as they clearly distinguish the quantities of liquid height, flow rate, and liquid volume in a hydraulic system.
Question 3:
|
One of the fundamental principles of calculus is a process called integration. This principle is important to understand because it is manifested in the behavior of capacitance. Thankfully, there are more familiar physical systems which also manifest the process of integration, making it easier to comprehend.
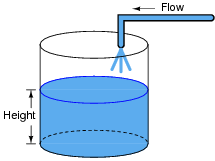
If we introduce a constant flow of water into a cylindrical tank with water, the water level inside that tank will rise at a constant rate over time:
|
|
In calculus terms, we would say that the tank integrates water flow into water height. That is, one quantity (flow) dictates the rate-of-change over time of another quantity (height).
Like the water tank, electrical capacitance also exhibits the phenomenon of integration with respect to time. Which electrical quantity (voltage or current) dictates the rate-of-change over time of which other quantity (voltage or current) in a capacitance? Or, to re-phrase the question, which quantity (voltage or current), when maintained at a constant value, results in which other quantity (current or voltage) steadily ramping either up or down over time?
Challenge question: can you think of a way we could exploit the similarity of capacitive voltage/current integration to simulate the behavior of a water tank's filling, or any other physical process described by the same mathematical relationship?
Notes:
The concept of integration doesn't have to be overwhelmingly complex. Electrical phenomena such as capacitance and inductance may serve as excellent contexts in which students may explore and comprehend the abstract principles of calculus. The amount of time you choose to devote to a discussion of this question will depend on how mathematically adept your students are.
Hopefully, the challenge question will stir your students' imaginations, as they realize the usefulness of electrical components as analogues for other types of physical systems.
Question 4:
Suppose two wires, separated by an air gap, are connected to opposite terminals on a voltage source (such as a battery). An electric field will develop in the space between the two wires: an invisible web of interaction, similar in some ways to a magnetic field. In this diagram, draw the invisible "lines of flux" for this electric field, showing their physical range:
|
|

|
|
Follow-up question: explain how electric flux lines differ in geometry from magnetic flux lines.
Notes:
Students may note that electric lines of flux do not follow the same paths that magnetic lines of flux would. Whereas magnetic lines of flux are always circular, electric lines of flux always terminate between points.
Note to your students the relevance of this fact in shielding: unlike magnetic shields which must divert the inevitable paths of magnetic flux lines, electric shields are able to terminate electric flux lines.
Question 5:
Electric fields may be described as ïnvisible webs" of interaction across space between electrically charged objects. Most people should be familiar with magnetic fields from playing with magnets as children: the forces of attraction or repulsion that act across open space between two or more magnetic objects. But electric fields are not the same as magnetic fields. The two different kinds of fields exert forces on entirely different objects.
Give an example of where an electric field manifests a tangible, physical force, like the magnetic fields we are all familiar with. Under what conditions are electric fields strong enough for human beings to detect without instruments?
In both cases, what condition causes such a strong electric field to develop?
Notes:
Electric field force is also used in some precision voltage measuring instruments (ëlectrostatic" meter movements), as well as the more common electroscope. If you happen to have either an electrostatic meter movement or an electroscope available in your classroom, use it to demonstrate the physical effects of electric fields.
Question 6:
Capacitance is a very important property in many types of electric circuits. Define what "capacitance" is, and what causes it.
Capacitance is caused by the establishment of an electric field between two conductors.
Notes:
Ask students what unit of measurement capacitance is expressed in. Also, ask them if they think the capacitance of any given conductor pair changes with the applied voltage or stored energy, or if capacitance is a quantity independent of particular electrical conditions.
Question 7:
The amount of capacitance between two conductors may be calculated by the following equation:
|
Where,
C = Capacitance in Farads
e = Permittivity of dielectric (absolute)
A = Conductor area, in square meters
d = Separation distance, in meters
How far away from each other would two metal plates, 2 square meters in area each, have to be in order to create a capacitance of 1 mF? Assume that the plates are separated by air.
Notes:
This problem is first and foremost an algebraic manipulation exercise. Then, it is merely a matter of solving for d given the proper values. Finding e could be difficult, though, and this is by design: I want students to learn the significance of absolute permittivity!
Question 8:
Capacitance exists between any two conductors separated by an insulating medium. Given this fact, it makes sense that a length of two-conductor electrical cable will have capacitance distributed naturally along its length:

|
|
There should be a way to prove the existence of such ßtray" capacitance in a substantial length of two-conductor cable. Devise an experiment to do this.
Notes:
The purpose of this question is to make students think critically and creatively about capacitance. There is more than one way to test for capacitance in a cable, so do not limit students to one method only!
Question 9:
Suppose you wished to build a component with no other purpose than to provide capacitance in an electric circuit (a capacitor). How might you design such a device to perform this function, and how could you maximize its capacitance?
To increase capacitance:
- �
- Increase plate area
- �
- Decrease spacing between plates
- �
- Increase permittivity of dielectric
Notes:
These factors affecting capacitance are very hypothetical when dealing with fixed-value capacitors. After all, few people will ever have to design or construct a capacitor. However, these factors are very practical and important to understand when dealing with stray capacitance between conductors, where conductor layout and placement are well within the control of those building an electrical system!
These factors are also important to understand for comprehending the function of variable capacitors. Be sure to bring up the subject of variable capacitors in your discussion with students.
Question 10:
What is a Leyden Jar, and how it its construction similar to the construction of all capacitors?
All capacitors share a common design feature of Leyden jars: the separation of two conductive plates by an insulating medium.
Notes:
Encourage your students to find a picture of a Leyden Jar, or even to build their own. One can't help but notice the functional equivalence between a capacitor and a jar: storing charge versus storing substance!
A jar is not the only object which may be transformed into a capacitor. Aluminum foil and paper sheets may also be used to make a rudimentary capacitor. Have your students experiment with building their own capacitors, especially if they have access to a capacitance meter which may be used to compare the capacitance of different designs.
Question 11:
Electric fields, like all fields, have two fundamental measures: field force and field flux. In a capacitor, which of these field quantities is directly related to voltage between the plates, and which is directly related to the amount of charge (in coulombs) stored?
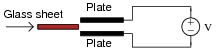
Based on this relationship, which electric field quantity changes when a sheet of glass is inserted between these two metal plates, connected to a source of constant voltage?
|
|
If a sheet of glass is inserted between two metal plates connected to a constant voltage source, the electric field force between the plates will remain unchanged, while the electric field flux will increase (and along with it, the amount of charge stored on the plates).
Follow-up question: explain how the variable of electric permittivity is relevant to the described situation.
Notes:
The concept of a field is quite abstract. Electric fields in particular are abstract because they cannot be tangibly perceived, at least not outside of dangerous voltage levels. Magnetic fields, which everyone should be familiar with from playing with magnets, may serve as an illustration of fields in general, but it is very important for students of electricity and electronics to understand that electric and magnetic fields are two different entities, albeit closely related (by Maxwell's Laws).
Question 12:
The storage of electric charge in a capacitor is often likened to the storage of water in a vessel:

|
|
Complete this analogy, relating the electrical quantities of charge (Q), voltage (E or V), and capacitance (C) to the quantities of water height, water volume, and vessel dimensions.
Voltage � Height of water column in vessel
Capacitance � Area of vessel, measured on a cross-section with a horizontal plane
Notes:
Many students find this a helpful analogy of capacitor action. But it helps even more if students work together to build the analogy, and to truly understand it.
Perform some "thought experiments" with vessels of different size, relating the outcomes to charge storage in capacitors of different size.
Question 13:
Suppose a mass is connected to a winch by means of a cable, and a person turns the winch drum to raise the mass off the ground:
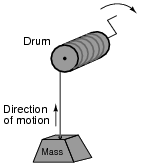
|
|
A physicist would likely look at this scenario as an example of energy exchange: the person turning the drum is expending energy, which in turn is being stored in the mass in potential form.
Suppose now that the person stops turning the drum and instead engages a brake mechanism on the drum so that it reverses rotation and slowly allows the mass to return to ground level. Once again, a physicist would view this scenario as an exchange of energy: the mass is now releasing energy, while the brake mechanism is converting that released energy into heat:
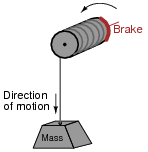
|
|
In each of the above scenarios, draw arrows depicting directions of two forces: the force that the mass exerts on the drum, and the force that the drum exerts on the mass. Compare these force directions with the direction of motion in each scenario, and explain how these directions relate to the mass and drum alternately acting as energy source and energy load.
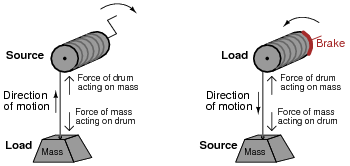
|
|
Follow-up question: although it may not be obvious, this question closely relates to the exchange of energy between components in electrical circuits! Explain this analogy.
Notes:
Students typically find the concept of energy flow confusing with regard to electrical components. I try to make this concept clearer by using mechanical analogies, in which force and motion act as analog quantities to voltage and current (or visa-versa).
Question 14:
Draw the direction of current in this circuit, and also identify the polarity of the voltage across the battery and across the resistor. Then, compare the battery's polarity with the direction of current through it, and the resistor's polarity with the direction of current through it.

|
|
What do you notice about the relationship between voltage polarity and current direction for these two different types of components? Identify the fundamental distinction between these two components that causes them to behave differently.

|
|
Whichever notation you choose to follow in your analysis of circuits, the understanding should be the same: the reason voltage polarities across the resistor and battery differ despite the same direction of current through both is the flow of power. The battery acts as a source, while the resistor acts as a load.
Notes:
This type of distinction is very important in the study of physics as well, where one must determine whether a mechanical system is doing work or whether work is being done on it. A clear understanding of the relationship between voltage polarity and current direction for sources and loads is very important for students to have before they study reactive devices such as inductors and capacitors!
Question 15:
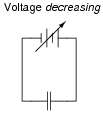
Suppose a capacitor is connected directly to an adjustable-voltage source, and the voltage of that source is steadily increased over time. We know that an increasing voltage across a capacitor will produce an electric field of increasing strength. Does this increase in electric field constitute an accumulation of energy in the capacitor, or a release of energy from the capacitor? In this scenario, does the capacitor act as a load or as a source of electrical energy?
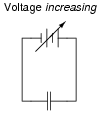
|
|
Now, suppose the adjustable voltage source is steadily decreased over time. We know this will result in an electric field of decreasing strength in the capacitor. Does this decrease in electric field constitute an accumulation of energy in the capacitor, or a release of energy from the capacitor? In this scenario, does the capacitor act as a load or as a source of electrical energy?
|
|
For each of these scenarios, label the direction of current in the circuit.
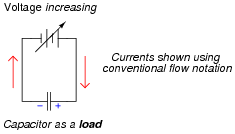
|
|
As the applied voltage decreases, the capacitor acts as a source, releasing accumulated energy to the rest of the circuit, as though it were a voltage source itself of superior voltage. Acting as a source, the current going "through" the capacitor will be in the same direction as through a battery, powering a load.
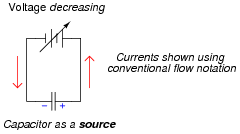
|
|
Notes:
Relating the direction of current in a capacitor to a change of applied voltage over time is a complex concept for many students. Since it involves rates of change over time, it is an excellent opportunity to introduce calculus concepts ([d/dt]).
Vitally important to students' conceptual understanding of a capacitor exposed to increasing or decreasing voltages is the distinction between an electrical energy source versus a load. Students need to think "battery" and "resistor," respectively when determining the relationship between direction of current and voltage drop. The complicated aspect of capacitors (and inductors!) is that they may switch character in an instant, from being a source of energy to being a load, and visa-versa. The relationship is not fixed as it is for resistors, which are always energy loads.
Question 16:
|
Ohm's Law tells us that the amount of current through a fixed resistance may be calculated as such:
|
We could also express this relationship in terms of conductance rather than resistance, knowing that G = 1/R:
|
However, the relationship between current and voltage for a fixed capacitance is quite different. The Öhm's Law" formula for a capacitor is as such:
|
What significance is there in the use of lower-case variables for current (i) and voltage (e)? Also, what does the expression [de/dt] mean? Note: in case you think that the d's are variables, and should cancel out in this fraction, think again: this is no ordinary quotient! The d letters represent a calculus concept known as a differential, and a quotient of two d terms is called a derivative.
Follow-up question: manipulate this equation to solve for the other two variables ([de/dt] = � ; C = �).
Notes:
I have found that the topics of capacitance and inductance are excellent contexts in which to introduce fundamental principles of calculus to students. The time you spend discussing this question and questions like it will vary according to your students' mathematical abilities.
Even if your students are not ready to explore calculus, it is still a good idea to discuss how the relationship between current and voltage for a capacitance involves time. This is a radical departure from the time-independent nature of resistors, and of Ohm's Law!
Question 17:
Complete this statement by substituting the correct electrical variables (voltage, current, resistance, capacitance):
- Capacitors oppose changes in (fill-in-the-blank), reacting to such changes by producing a (fill-in-the-blank).
Notes:
Emphasize to your students that capacitance is an essentially reactive property, opposing change in voltage over time. It is not steady voltage that capacitors react to, only changing voltage.
Question 18:
Electrical capacitance has a close mechanical analogy: elasticity. Explain what the term ëlasticity" means for a mechanical spring, and how the quantities of velocity and force applied to a spring are respectively analogous to current and voltage applied to a capacitance.
|
Where,
v = Velocity of spring compression
k = Spring ßtiffness" constant
F = Reaction force generated by the spring's compression
t = Time
In a similar manner, a pure capacitance experiencing a constant current will exhibit a constant rate of voltage change over time:
|
Notes:
Note to your students that spring stiffness (k) and capacitance (C) are inversely proportional to one another in this analogy.
Explain to your students how the similarities between inertia and capacitance are so close, that capacitors can be used to electrically model mechanical springs!
Question 19:
|
Capacitors store energy in the form of an electric field. We may calculate the energy stored in a capacitance by integrating the product of capacitor voltage and capacitor current (P = IV) over time, since we know that power is the rate at which work (W) is done, and the amount of work done to a capacitor taking it from zero voltage to some non-zero amount of voltage constitutes energy stored (U):
|
|
|
Find a way to substitute capacitance (C) and voltage (V) into the integrand so you may integrate to find an equation describing the amount of energy stored in a capacitor for any given capacitance and voltage values.
|
Notes:
The integration required to obtain the answer is commonly found in calculus-based physics textbooks, and is an easy (power rule) integration.
