Home » Worksheets

Decibel measurements

Question 1:

During the early development of telephone technology, a unit was invented for representing power gain (or loss) in an electrical system. It was called the Bel, in honor of Alexander Graham Bell, the telecommunications pioneer.
"Bels" relate to power gain ratios by the following equation:

A_P(ratio) = 10^A_P(Bels)

Given this mathematical relationship, translate these power gain figures given in units of Bels, into ratios:

�: A_P = 3 B ; A_P =
�: A_P = 2 B ; A_P =
�: A_P = 1 B ; A_P =
�: A_P = 0 B ; A_P =
�: A_P = -1 B ; A_P =
�: A_P = -2 B ; A_P =
�: A_P = -3 B ; A_P =

�: A_P = 3 B ; A_P = 1000
�: A_P = 2 B ; A_P = 100
�: A_P = 1 B ; A_P = 10
�: A_P = 0 B ; A_P = 1
�: A_P = -1 B ; A_P = [1/10]
�: A_P = -2 B ; A_P = [1/100]
�: A_P = -3 B ; A_P = [1/1000]

Follow-up question: a geologist, taking a class on electronics, sees this mathematical pattern and remarks, "This is just like the Richter scale!" Explain what the geologist means.

Notes:
Ask your students how these two systems of power gain expression (Bels versus ratios) compare in terms of range. Which system of expression encompasses the greatest range of power gains or losses, with the smallest changes in numerical value?

Question 2:

Manipulate this equation algebraically, so that we can convert power gains expressed in units of Bels, into ratios.

A_P(ratio) = 10^A_P(Bels)

Then, convert the following power gains, expressed as ratios, into units of Bels:

�: A_P = 250 ; A_P =
�: A_P = 1275 ; A_P =
�: A_P = 10 ; A_P =
�: A_P = 1 ; A_P =
�: A_P = 0.1 ; A_P =
�: A_P = 0.025 ; A_P =
�: A_P = 0.00009 ; A_P =

A_P(Bels) = logA_P(ratio)

�: A_P = 250 ; A_P = 2.398 B
�: A_P = 1275 ; A_P = 3.106 B
�: A_P = 10 ; A_P = 1 B
�: A_P = 1 ; A_P = 0 B
�: A_P = 0.1 ; A_P = -1 B
�: A_P = 0.025 ; A_P = -1.602 B
�: A_P = 0.00009 ; A_P = -4.046 B

Notes:
Challenge your students to estimate the log values without using their calculators. For example, they should be able to estimate the log of 1275 as being between 3 and 4; the log of 0.025 as being between -1 and -2. Work together to devise a technique for doing this, where there will be no guessing.
Mathematical estimation is an important skill for technical people to possess. Not only is it useful in the event no calculator is readily available, but it also helps greatly in students being able check their (electronically) calculated work. I can't tell you how many times I've seen students blindly enter numbers into a calculator, only to arrive at an answer that is grossly in error, and not realize it at all because they cannot do the estimation mentally.

Question 3:

At some point in time, it was decided that the unit of the "Bel" was too large. Instead, the deci-Bel became the most common usage of the unit. Modify these equations to include A_P figures cast in units of decibels (dB) instead of Bels:

A_P(ratio) = 10^A_P(Bels)

A_P(Bels) = logA_P(ratio)

Then, calculate the decibel figures that correspond to a power gain of 2 (ratio), and a power loss of 50%, respectively.

A_P(ratio) = 10^{[(A_P(dB))/10]}

A_P(dB) = 10 logA_P(ratio)

Power gain of 2 (ratio) � 3 dB
Power loss of 50% (ratio) � -3 dB

Notes:
It is important that students work through the original equations algebraically to obtain the answers rather than just look up these formulae in a book. Have your students write their work on the whiteboard in front of the other students, so that everyone has the opportunity to examine the technique(s) and ask pertinent questions.
Be sure to let your students know that the figure of "3 dB", either positive or negative, is very common in electronics calculations. Your students might remember this expression used to describe the cutoff frequency of a filter circuit (f_{-3 dB}).

Question 4:

Suppose an AC signal amplifier circuit has a voltage gain (ratio) of 2. That is, V_out is twice as large as V_in:

If we were to try to rate this amplifier's gain in terms of the relative power dissipated by a given load resistance (P_load when powered by V_out, versus P_load when powered by V_in), what ratio would we calculate? In other words, what is the ratio of power for a given load resistance, when powered by a given voltage, versus when powered by a voltage that is twice as much?

Power ratio = 4:1

Notes:
An easy way to illustrate this principle is to ask your students to calculate the power dissipation of a 1200 watt heating element rated for 120 volts, if connected to a 240 volt source. The answer is not 2400 watts!

Question 5:

Suppose an AC signal amplifier circuit has a voltage gain (ratio) of 2. That is, V_out is twice as large as V_in:

If we were to try to rate this amplifier's gain in terms of the relative power dissipated by a given load resistance (P_load when powered by V_out, versus P_load when powered by V_in), what decibel figure would we calculate?

A_P = 6.02 dB

Notes:
An easy way to illustrate this principle is to ask your students to calculate the power dissipation of a 1200 watt heating element rated for 120 volts, if connected to a 240 volt source. The answer is not 2400 watts!

Question 6:

Voltage and current gains, expressed in units of decibels, may be calculated as such:

A_V(dB) = 10 log( A_V(ratio) ) ²

A_I(dB) = 10 log( A_I(ratio) ) ²

Another way of writing this equation is like this:

A_V(dB) = 20 logA_V(ratio)

A_I(dB) = 20 logA_I(ratio)

What law of algebra allows us to simplify a logarithmic equation in this manner?

loga^b = b loga

Challenge question: knowing this algebraic law, solve for x in the following equation:

520 = 8^x

Notes:
Logarithms are a confusing, but powerful, algebraic tool. In this example, we see how the logarithm of a power function is converted into a simple multiplication function.
The challenge question asks students to apply this relationship to an equation not containing logarithms at all. However, the fundamental rule of algebra is that you may perform any operation (including logarithms) to any equation so long as you apply it equally to both sides of the equation. Logarithms allow us to take an algebra problem such as this and simplify it significantly.

Question 7:

Convert the following amplifier gains (either power, voltage, or current gain ratios) into gains expressed in the unit of decibels (dB):

�: A_P = 25 ; A_P(dB) =
�: A_V = 10 ; A_V(dB) =
�: A_I = 37 ; A_I(dB) =
�: A_P = 150 ; A_P(dB) =
�: A_I = 41 ; A_I(dB) =
�: A_V = 3.4 ; A_V(dB) =
�: A_P = 18 ; A_P(dB) =
�: A_V = 100 ; A_V(dB) =

�: A_P = 25 ; A_P(dB) = 13.98 dB
�: A_V = 10 ; A_V(dB) = 20 dB
�: A_I = 37 ; A_I(dB) = 31.36 dB
�: A_P = 150 ; A_P(dB) = 21.76 dB
�: A_I = 41 ; A_I(dB) = 32.26 dB
�: A_V = 3.4 ; A_V(dB) = 10.63 dB
�: A_P = 18 ; A_P(dB) = 12.55 dB
�: A_V = 100 ; A_V(dB) = 40 dB

Notes:
Nothing special here, just straightforward ratio-to-decibel calculations. Have your students share and discuss the steps necessary to do all these conversions.

Question 8:

Convert the following amplifier gains expressed in the unit of decibels (dB), to gain figures expressed as unitless ratios:

�: A_P = 5 dB ; A_P(ratio) =
�: A_V = 23 dB ; A_V(ratio) =
�: A_I = 20 dB ; A_I(ratio) =
�: A_P = 2.5 dB ; A_P(ratio) =
�: A_I = 7.4 dB ; A_I(ratio) =
�: A_V = 45 dB ; A_V(ratio) =
�: A_P = 12.8 dB ; A_P(ratio) =
�: A_V = 30 dB ; A_V(ratio) =

�: A_P = 5 dB ; A_P(ratio) = 3.16
�: A_V = 23 dB ; A_V(ratio) = 14.13
�: A_I = 20 dB ; A_I(ratio) = 10
�: A_P = 2.5 dB ; A_P(ratio) = 1.78
�: A_I = 7.4 dB ; A_I(ratio) = 2.34
�: A_V = 45 dB ; A_V(ratio) = 177.8
�: A_P = 12.8 dB ; A_P(ratio) = 19.05
�: A_V = 30 dB ; A_V(ratio) = 31.62

Notes:
Nothing special here, just straightforward decibel-to-ratio calculations. Have your students share and discuss the steps necessary to do all these conversions.

Question 9:

Convert the following amplifier gains between decibels and (unitless) ratios as necessary:

�: A_V = 14.1 dB ; A_V(ratio) =
�: A_I = 202 ; A_I(dB) =
�: A_P = 15 dB ; A_P(ratio) =
�: A_I = 33 ; A_I(dB) =
�: A_P = 49 dB ; A_P(ratio) =
�: A_V = 57 ; A_V(dB) =
�: A_P = 8.8 dB ; A_P(ratio) =
�: A_V = 30 ; A_V(dB) =

�: A_V = 14.1 dB ; A_V(ratio) = 5.07
�: A_I = 202 ; A_I(dB) = 46.1 dB
�: A_P = 15 dB ; A_P(ratio) = 31.62
�: A_I = 33 ; A_I(dB) = 30.37 dB
�: A_P = 49 dB ; A_P(ratio) = 79,432
�: A_V = 57 ; A_V(dB) = 35.12 dB
�: A_P = 8.8 dB ; A_P(ratio) = 7.59
�: A_V = 30 ; A_V(dB) = 29.54 dB

Notes:
Nothing special here, just straightforward decibel-ratio calculations. Have your students share and discuss the steps necessary to do all these conversions.

Question 10:

What does it mean to speak of the gain of a circuit? This term is very commonly used when describing amplifier circuits, but it may also be used to describe circuits containing nothing but passive components, and are thus incapable of amplifying.
What letter is used to symbolize gain in mathematical equations?

"Gain" (A) refers to the ratio of output signal compared to input signal.

Notes:
Discuss what it means for a circuit to have a designated öutput" and ïnput". Can they think of any circuits studied thus far that have places to input and output signals?

Question 11:

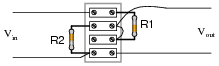
Calculate the voltage gain of this circuit, if R1 has a resistance of 8.1 kW and R2 has a resistance of 1.75 kW:

A_V = 0.178
Follow-up question: how does this gain figure (A_V) relate to the "voltage divider formula"?

E_R = E_total

�
�

R

R_total

�
�

Notes:
Students should readily recognize this circuit as a voltage divider, from their education in basic DC circuits. Though it may seem strange to calculate the "gain" of a completely passive and indeed dissipative circuit, it is entirely valid.
Discuss with your students the maximum and minimum possible power gain values for a circuit of this type.

Question 12:

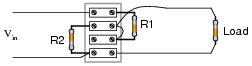
Calculate the power gain of this circuit, if R1 has a resistance of 1 kW, R2 has a resistance of 5.1 kW, and the load has a resistance of 10 kW:

A_P = 0.261
Follow-up question: what unit does this figure have, if any?

Notes:
Students should readily recognize this circuit from their education in basic DC circuits. Though it may seem strange to calculate the "gain" of a completely passive and indeed dissipative circuit, it is entirely valid.
Discuss with your students the maximum and minimum possible power gain values for a circuit of this type. Also discuss with them the nature of ratios with regard to units.

Question 13:

Suppose an AC signal amplifier circuit has a voltage gain (ratio) of 5. That is, V_out is five times as large as V_in:

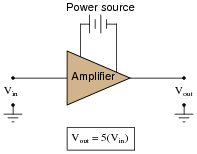
Translate this voltage gain ratio into a decibel figure. Explain why the conversion from voltage gain ratio to decibels is not the same as conversion of a power gain ratio to decibels.

A_V = 13.98 dB

Notes:
Discuss with your students the nature of the "Bel" unit: it is fundamentally a unit of power gain, not voltage or current gain. So, representing voltage or current gains in units of either Bels or decibels means representing those voltage or current gains in terms of how much power gain they equate to.

Question 14:

Specialized forms of the decibel unit have been devised to allow easy representation of quantities other than arbitrary ratios of voltage, current, or power. Take for example these units, the first one used extensively in the telecommunications industry:

�: dBm
�: dBW
�: dBk

Define what each of these units represents.

"dBm" represents the magnitude of a voltage in relation to 1 mW of power dissipated by a 600 W load. "dBW" and "dBk" units represent the magnitude of a voltage in relation to 1 W and 1 kW of power dissipated by the same load, respectively.
Follow-up question: how many volts is 2 dBm equivalent to?

Notes:
Here we see the decibel unit being used to represent absolute quantities rather than relative ratios. Ask your students what benefit would there be in doing this. Why not just represent signal magnitudes in units of "volts" instead? Why would we want to use an obscure unit such as the decibel?

Question 15:

Calculate the overall voltage gain of this cascaded amplifier circuit, where the output of one voltage amplifier feeds into the input of another:

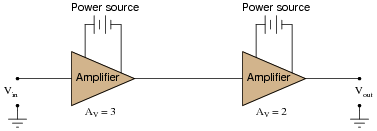
Also, convert the voltage gains of each amplifier into units of decibels, then convert the overall voltage gain ratio into units of decibels as well.
What do you notice about the overall gain of this circuit in relation to the individual amplifier gains, compared as ratios versus compared as decibel figures?

Cascaded voltage gains expressed as ratios:

A_V = 3 ×2 = 6

Cascaded voltage gains expressed a decibel figures:

A_V = 9.54 dB + 6.02 dB = 15.56 dB

Notes:
Besides providing practice with ratio-to-decibel conversions, the purpose of this question is for students to realize that gains multiply as ratios but add as decibels.

Question 16:

Calculate the overall voltage gain of this cascaded amplifier circuit, where the output of one voltage amplifier feeds into the input of another:

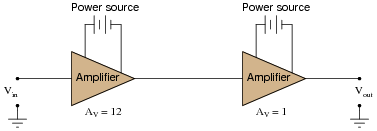
Also, convert the voltage gains of each amplifier into units of decibels, then convert the overall voltage gain ratio into units of decibels as well.
What do you notice about the overall gain of this circuit in relation to the individual amplifier gains, compared as ratios versus compared as decibel figures?

Cascaded voltage gains expressed as ratios:

A_V = 12 ×1 = 12

Cascaded voltage gains expressed a decibel figures:

A_V = 21.58 dB + 0 dB = 21.58 dB

Notes:
Besides providing practice with ratio-to-decibel conversions, the purpose of this question is for students to realize that gains multiply as ratios but add as decibels.

Question 17:

In this cascaded voltage divider circuit, determine the overall voltage gain ratio (from first input to last output), and also calculate the overall voltage gain in decibels, as well as the decibel figure for each divider's voltage gain:

What do you notice about the ratio figures versus the decibel figures, regarding how the individual stage gains compare with the overall gain?

Notes:
Discuss with your students the nature of cascaded gain figures in both ratio and decibel formats. Which format is easier to calculate manually (without using a calculator)? Why is this?

Question 18:

In this circuit, one amplifier feeds into an attenuator circuit, which then feeds into a second amplifier stage. Calculate the "gain" of the attenuator, and then calculate the overall voltage gain of this three-stage circuit:

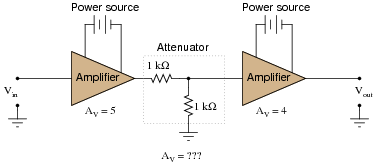
Also, convert the voltage gains of each stage into units of decibels, then convert the overall voltage gain ratio into units of decibels as well.
What do you notice about the overall gain of this circuit in relation to the individual amplifier gains, compared as ratios versus compared as decibel figures?

Cascaded voltage gains expressed as ratios:

A_V = 5 ×

�
�

1

2

�
�

×4 = 10

Cascaded voltage gains expressed a decibel figures:

A_V = 13.98 dB + (-6.02 dB) + 12.04 = 20 dB

Notes:
Besides providing practice with ratio-to-decibel conversions, the purpose of this question is for students to realize that gains multiply as ratios but add as decibels.

Question 19:

Calculate the necessary gain of the second-stage amplifier to give the whole circuit a voltage gain of 25 decibels, then translate all decibel figures into gain ratios:

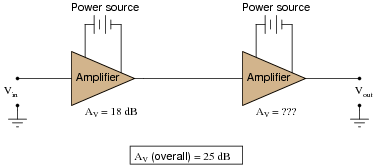
�: Stage 1 gain = 18 dB = 7.94
�: Stage 2 gain = 7 dB = 2.24
�: Overall gain = 25 dB = 17.8

Notes:
This question is nothing more than "drill" for students to practice decibel/ratio conversions.