Inductors
Question 1:
|
A 5 H inductor is subjected to an electric current that changes at a rate of 4.5 amps per second. How much voltage will be dropped by the inductor?
Notes:
Don't give your students the equation with which to perform this calculation! Let them find it on their own. The [di/dt] notation may be foreign to students lacking a strong mathematical background, but don't let this be an obstacle to learning! Rather, use this as a way to introduce those students to the concept of rates of change, and to the calculus concept of the derivative.
Question 2:
|
Suppose an inductor is connected to a variable current source, where the current is steadily increased at a rate of 1.5 amps per second. How much voltage will the 4 Henry inductor drop, and what will be the polarity of that drop? Remember, the direction of the arrow in a current source symbol points in the direction of conventional flow, not electron flow!
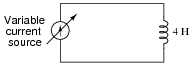
|
|
In real life, an inductor will not drop the exact same amount of voltage that you will calculate here. Determine if the real voltage drop across such an inductor would be greater or less than predicted, and explain why.

|
|
In real life, through, the inductor would drop more than 6 volts, due to winding resistance.
Follow-up question: research the typical winding resistance of a 4 henry inductor.
Notes:
Ahhh, the controversy of conventional versus electron flow. The existence of two contradicting conventions for denoting direction of electric current irritates me to no end, especially when the one upon which almost all electronic device symbolism is based on is actually incorrect with regard to charge flow through metallic conductors (the majority case in electric circuits)! Your students will surely encounter both "conventional" and ëlectron" flow in their careers, so be sure to introduce them to both conventions.
Discuss with your students the consequences of winding resistance in real inductors. Is it significant? Work together with your students to calculate how much extra voltage would be dropped across the inductor, based on their research on the typical winding resistance of a 4 henry inductor (ask them where they obtained the information!), given a [di/dt] rate of 1.5 amps per second.
Ask your students if they think it might be possible to create an inductor with no ßtray" resistance at all to interfere with perfect, theoretical inductor behavior. What would be required to make the "perfect" inductor?
Question 3:
Two 5 H inductors connected in series are subjected to an electric current that changes at a rate of 4.5 amps per second. How much voltage will be dropped across the series combination?
Now suppose that two 5 H inductors connected in parallel are subjected to the same total applied current (changing at a rate of 4.5 amps per second). How much voltage will be dropped by these inductors? Hint: the total current is divided evenly between the two inductors.
Follow-up question: what do these figures indicate about the nature of series-connected and parallel connected inductors? In other words, what single inductor value is equivalent to two series-connected 5 H inductors, and what single inductor value is equivalent to two parallel-connected 5 H inductors?
Notes:
If your students are having difficulty answering the follow-up question in the Answer, ask them to compare these voltage figures (45 V and 11.25 V) against the voltage that would be dropped by just one of the 5 H inductors under the same condition (an applied current changing at a rate of 4.5 amps per second).
It is, of course, important that students know how series-connected and parallel connected inductors behave. However, this is typically a process of rote memorization for students rather than true understanding. With this question, the goal is to have students come to a realization of inductor connections based on their understanding of series and parallel voltages and currents.
Question 4:
Suppose two 50 mH inductors are connected in parallel with each other. What will their combined inductance be, in Henrys? Explain your answer.
Notes:
Ask your students this question: given capacitors and inductors, which of these component types behave more like resistors, in terms of their series versus parallel equivalent values?
Question 5:
Calculate the total inductance in this collection of inductors, as measured between the two wires:

|
|
Also, write a formula that calculates total inductance given the values of inductors L1, L2, and L3.
Note: the following formula is not the only possible one for describing total inductance in this circuit!
|
Notes:
It is most helpful to first draw a schematic diagram for this inductor network before trying to perform any inductance calculations, in order that a clear understanding of the series/parallel connections be established.
Question 6:
How large must inductor Lx be in order to provide a total inductance of 2.5 H in this network of inductors?
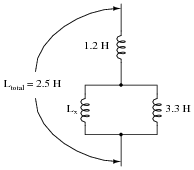
|
|
Notes:
Inductors tend to be even more scarce than resistors in regard to the availability of different values, so knowing how to combine different inductors together to achieve a desired total inductance is a practical skill.
It should be noted to your students that inductors may interact with one another if placed too close, due to the magnetic field of one inductor "linking" with the coil of another inductor. This is called mutual inductance, and if present alters the otherwise straightforward series-parallel inductance relationships that one would expect to be analogous to series-parallel resistances.
Question 7:
Suppose a short-circuit were to develop in this electric power system:

|
|
The purpose of the circuit breaker, of course, is to open the circuit automatically, to prevent damage to the power conductors. In a large electric power system, the magnitudes of such short-circuit currents can be enormous.
Large inductors, commonly called reactors, are often installed in series with power conductors in high-voltage power systems in order to ßoften" the onset of short-circuit currents:

|
|
Explain how the addition of a "reactor" helps to minimize the magnitude of the short-circuit current the breaker has to interrupt.
Follow-up question: why use an inductor to limit the short-circuit fault current? Why not use a resistor instead?
Notes:
Power system reactors are usually installed in substations, where they appear as coils of wire (no iron core) a few feet in diameter, usually located near circuit breakers.
Question 8:
Small inductors often look like resistors, even to the extent that their values are designated by colored bands. Determine the values of the following inductors (express the tolerance as a percentage), based on their color codes:
- �
- Red, Grn, Brn, Gld
- �
- Wht, Org, Red, Sil
- �
- Grn, Gry, Blk
- �
- Vio, Blu, Org, Gld
- �
- Red, Grn, Brn, Gld = 250 mH, +/- 5%
- �
- Wht, Org, Red, Sil = 9300 mH, +/- 10%
- �
- Grn, Gry, Blk = 58 mH, +/- 20%
- �
- Vio, Blu, Org, Gld = 76 mH, +/- 5%
Notes:
Students will note a lot of similarities between the inductor color code and the resistor color code, but they should also note one significant difference!
Question 9:
When checked with an ohmmeter, how should a properly functioning inductor respond?
Follow-up question: what do you suppose is the most likely failure "mode" of an inductor, open or shorted? Explain your answer.
Notes:
Have your students actually test a few inductors with their ohmmeters in class. Unlike capacitor checking with an ohmmeter, there is never a substantial "charging" period! If your students have already learned about capacitor checking with an ohmmeter, ask them to explain why there is no "charging" action indicated by the ohmmeter when connected to an inductor.
If there were an observable "charging" time exhibited by an inductor when measured by an ohmmeter, what would it appear as, in terms of the ohmmeter's indication?
Normally, I don't give away answers to follow-up questions in the "Notes" section, but here I feel it may be necessary. Studies have shown that inductors have about an equal chance of failing open as they do failing shorted. Of course, this will vary with the specific design and application of the inductor, but there is no mode of failure clearly more probable than the other.
Question 10:
|
What happens to the inductance of an inductor as its core becomes saturated? Does the inductance value increase, decrease, or remain the same? Explain your answer.
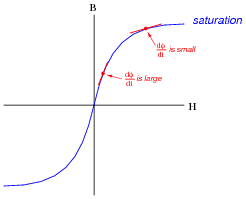
|
|
This causes the inductance to decrease.
Notes:
Ask your students to identify what condition(s) might lead to a condition of saturation. And, even if the extreme ends of the B-H curve are avoided, what does the nonlinear shape of the B-H plot indicate about the linearity of an inductor? The inductance formula (e = L[di/dt]) assumes perfect linearity, but is this really true for an inductor whose core exhibits this kind of magnetic flux/force relationship?
Question 11:
Find one or two real inductors and bring them with you to class for discussion. Identify as much information as you can about your inductors prior to discussion:
- �
- Inductance (ideal)
- �
- Inductance (actual)
- �
- Winding resistance
- �
- Current rating
- �
- Type (iron core, air core, etc.)
Be prepared to prove the actual winding resistance of your inductors in class, by using a multimeter!
Notes:
The purpose of this question is to get students to kinesthetically interact with the subject matter. It may seem silly to have students engage in a ßhow and tell" exercise, but I have found that activities such as this greatly help some students. For those learners who are kinesthetic in nature, it is a great help to actually touch real components while they're learning about their function. Of course, this question also provides an excellent opportunity for them to practice interpreting component markings, use a multimeter, access datasheets, etc.
