Home » Worksheets

Latch circuits

Question 1:

What do you think this logic buffer gate will do, with the output signal "feeding back" to the input?

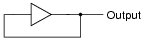
What do you think this buffer will do when each input switch is separately pressed?

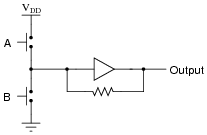
Why does the second buffer circuit need a resistor in the feedback loop?

The first circuit will "latch" in whatever logic state it powers up in. The second circuit will be ßet" or "reset" according to which pushbutton switch is actuated, then latch in that state when neither switch is being pressed. The resistor prevents the gate from ßeeing" a short circuit at its output when a pushbutton switch is actuated to change states.
Challenge question: how would you determine an appropriate size for the resistor? Don't just guess - base your answer on specific performance parameters of the gate!

Notes:
This is a very crude sort of latch circuit, but it is easier to understand than the typical cross-connected NOR or NAND gate latches commonly introduced to circuits. One of the major ideas in this question is the concept of positive feedback, and how this form of feedback leads to hysteretic behavior. If appropriate, refer your students to SCRs and other thyristors as previous examples of hysteretic devices based on positive feedback.

Question 2:

When studying latch circuits, you will come across many references to set and reset logic states. Give a simple definition for each of these terms in the context of latch and flip-flop circuits.

A latch is considered set when its output (Q) is high, and reset when its output (Q) is low.

Notes:
Having a consistent definition for ßet" and "reset" is important, especially as students study multiple latch circuit topologies and active-low inputs!

Question 3:

The circuit shown here is called an S-R latch:

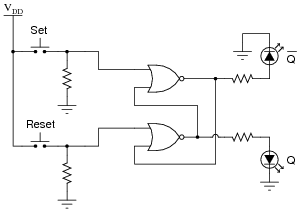
Complete the truth table for this latch circuit:

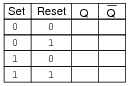
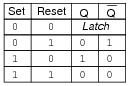
Follow-up question: The final state of this truth table (where the "Set" and "Reset" inputs are both high) is usually referred to as invalid. Explain why.

Notes:
The "latch" state is the most interesting in this circuit. Discuss what this means with your students, especially since it is impossible to describe the "latch" state in terms of fixed 1's and 0's.

Question 4:

Some digital circuits are considered to have active-low inputs, while others have active-high inputs. Explain what each of these terms means, and how we might identify which type of input(s) a digital circuit has.

An äctive-low" input is one where that particular gate function is activated or invoked on a low logic state. Active-low inputs are identified by inversion bubbles (or inversion wedges) drawn at the IC input terminals. For example, the Enable input (EN) for the following integrated circuit is active-low, meaning the chip is enabled when that input line is held at ground potential:

This S-R latch circuit has active-low preset ([`PRE]) and clear ([`CLR]) inputs, meaning the latch circuit will be preset and cleared when each of these inputs are grounded, respectively:

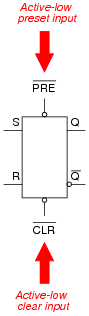
Active-high inputs, conversely, engage their respective functions when brought to power supply rail (V_DD or V_CC) potential. As one might expect, an active-high input will not have an inversion bubble or wedge next to the input terminal.
Challenge question: to the surprise of many students, there are a great number of digital logic circuit types built with active-low inputs. Explain why. Hint: most of these circuit types and functions were pioneered with TTL logic rather than CMOS logic.

Notes:
Active-low inputs tend to confuse many students, hence my unusually long and descriptive answer.

Question 5:

The circuit shown here is called an S-R latch:

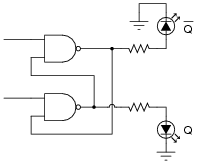
Identify which of the two input lines is the Set, and which is the Reset, and then write a truth table describing the function of this circuit.

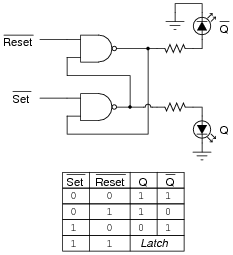
Follow-up question: why are the inputs referred to as [`Set] and [`Reset], rather than just Set and Reset?

Notes:
The "latch" state is the most interesting in this circuit. Discuss what this means with your students, especially since it is impossible to describe the "latch" state in terms of fixed 1's and 0's. Also ask your students to identify the ïnvalid" state of this latch circuit, and to explain why it is called ïnvalid".
Discuss the active-low nature of this latch circuit's inputs. Explain to your students that many digital functions have active-low inputs, and that it is common to denote those inputs by writing a Boolean complementation bar over the input's name.

Question 6:

Latch circuits are often drawn as complete units in their own block symbols, rather than as a collection of individual gates:

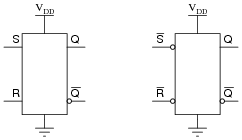
This simplifies schematic drawings where latches are used, much as the use of gate symbolism (as opposed to drawing individual transistors and resistors) simplifies the diagrams of more elementary digital circuits.
From the block symbols shown in this question, is there any way to determine which of the S-R latches is built with NOR gates, and which one is built with NAND gates?

This is a bit of a trick question. If NOR and NAND are the only gate choices available, then the left latch is made from NOR gates and the right latch is made from NAND gates. However, it is possible to make S-R latches out of gates other than NOR or NAND.
Challenge question: can you think of other gate types that could be used to build S-R latch circuits? Hint: there are at least two alternatives to NOR and NAND!

Notes:
If students become stuck on the challenge question, just whisper "DeMorgan's Theorem" to them and watch what happens!

Question 7:

The following relay logic circuit is for starting and stopping an electric motor:

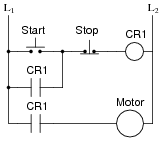
Draw the CMOS logic gate equivalent of this motor start-stop circuit, using these two pushbutton switches as inputs:

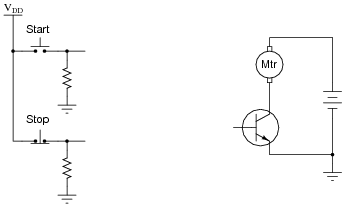
Make sure that your schematic is complete, showing how the logic gate will drive the electric motor (through the power transistor shown).

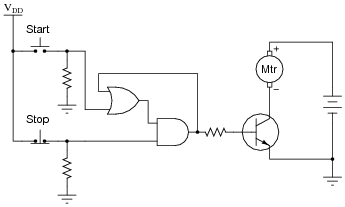
Follow-up question: why is the "Stop" switch always normally-closed in motor control circuits, whether it be relay logic or semiconductor logic? It is easy enough to invert a signal if we wish to, either by using a relay or by using a NOT gate, so shouldn't the choice of switch "normal" status be arbitrary?
Challenge question: why not operate the electric motor off the same V_DD power source that the gates are powered by? If we had to do such a thing, what circuit additions would you propose to minimize any potential trouble?

Notes:
Discuss the follow-up question with your students. Why is the "Stop" switch always normally-closed, if we have the freedom to choose normally-open contacts? Why not standardize the pushbutton switches, making them both the same type? The answer has to do with circuit faults, and what is considered the safest mode of failure.
I suspect many students will neglect to include the base resistor in their designs. This resistor is important, though, for the sake of the driving gate. You might even want to spend some class time with your students calculating an appropriate value of resistance, given such parameters as:

�: Motor "run" current = 300 mA
�: Transistor b = 50
�: V_DD = 6 volts DC

The challenge question may be too advanced for students who have not yet experienced the pains of trying to operate power devices and logic devices off the same DC bus. Suffice it to say, it is a good design rule to keep separate DC power supplies for logic and load circuitry, even if they are the exact same voltage!

Question 8:

One practical application of S-R latch circuits is switch debouncing. Explain what "bounce" refers to in mechanical switches, and also explain how this circuit eliminates it:

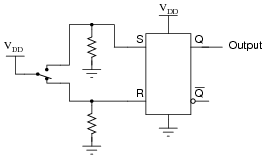
Also, show where an oscilloscope could be connected to display any switch "bounce," and explain how the oscilloscope would have to be configured to capture this transient event.

The "latching" ability of the S-R latch circuit holds the output state steady during the mechanical switch's bouncing action, allowing a "clean" output transition to take place.
Connecting the input probe of an oscilloscope to either the S or R input of the latch will show bounce, if it occurs. To capture this event, the 'scope would have to be configured for single-sweep mode, and have the triggering controls properly set. A digital storage oscilloscope is essential for this type of work!
Follow-up question: how do you suggest choosing appropriate pull-down resistor sizes for this circuit, or any CMOS circuit for that matter?

Notes:
Many textbooks use switch debouncing as a practical example of S-R latch function, so I won't bother giving hints as to how this circuit works. Let the students do their own research, and let them explain it to you during discussion.
If students need practical examples of how switch "bouncing" can be bad, suggest digital counter circuits, where a mechanical switch causes a counter to increment (or decrement) once per actuation. If the switch bounces, the counter will increment (or decrement) more than once per switch actuation, which is undesirable.
Oscilloscope triggering is one of those features that separates novice 'scope users from competent 'scope users. Anyone can learn to display a repetitive waveform on an oscilloscope with a minimum of adjustment. Many modern digital oscilloscopes even have äuto-configure" features to lock in such waveforms for display. However, to set up triggering on one-time events requires that the user understand not only the oscilloscope's functions, but also the nature of the event to be captured.
Note to your students how the [`Q] output of the latch doesn't go anywhere. Often, we have applications where the second output of a latch is unused. Ask your students whether or not this constitutes a problem. (If you get blank stares from asking this question, remind students that unused CMOS inputs have to be grounded or tied to V_DD, or else damage may occur. Ask them whether or not the same rule applies to gate outputs.) This will be a good review of internal gate circuit construction.

Question 9:

Complete the timing diagram, showing the state of the Q output over time as the Set and Reset switches are actuated. Assume that Q begins in the low state on power-up:

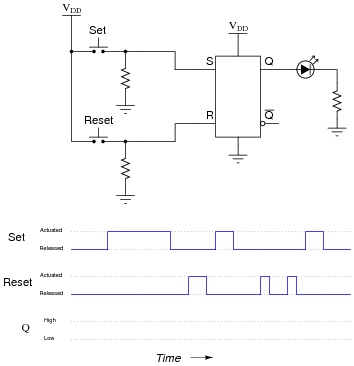
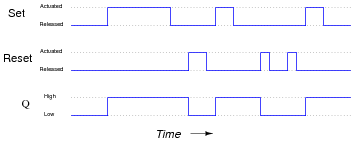
Follow-up question: complete a schematic diagram showing how the [`Q] output of the latch could turn on an electric motor through a bipolar junction transistor. Also, determine whether the latch circuit would be sourcing or sinking current to the transistor when the motor is running:

Notes:
Nothing special here in this question. Perhaps the main point is to familiarize students with the concept of a timing diagram, and how to transfer the truth table function of a specific logic circuit to a time-domain plot.

Question 10:

A student builds this simple S-R latch for their lab experiment:

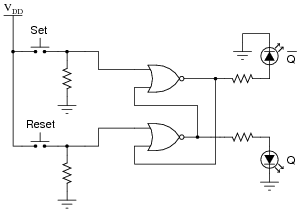
When the student powers up this circuit, she notices something strange. Sometimes the latch powers up in the set state (Q high and [`Q] low), and other times it powers up in the reset state (Q low and [`Q] high). The power-up state of their circuit seems to be unpredictable.
What state should their circuit power up in? Did the student make an error building the latch circuit?

The circuit is fine, and working properly. The normal power-up state of a latch circuit is unpredictable, so long as both the inputs are inactive.

Notes:
Although the circuit itself is simple, the phenomenon is not. Tell your students that what they're dealing with here is something called a race condition, where two or more gates try to "race" each other to reach a certain logic state. Analyze the power-up state of this circuit with your students, and they will see that an unstable condition exists when both inputs are inactive!

Question 11:

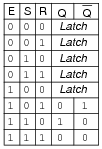
The circuit shown here is a gated S-R latch. Write the truth table for this latch circuit, and explain the function of the Ënable" (E) input:

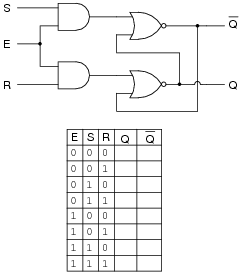
When the Enable input is low (0), the circuit ignores the Set and Reset inputs:

Notes:
Just one more level of gating added to an S-R latch circuit!

Question 12:

Here is an S-R latch circuit, built from NAND gates:

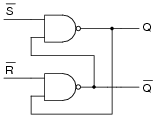
Add two more NAND gates to this circuit, converting it into a gated S-R latch, with an Enable (E) input, and write the truth table for the new circuit.

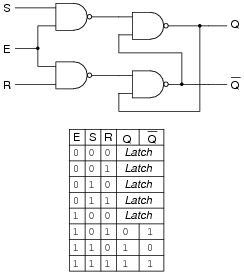
Follow-up question: explain why the inputs to the latch circuit are not active-low as they were before the addition of the two extra NAND gates. In other words, why does this latch now have S and R inputs rather than [`S] and [`R] inputs as it did before?

Notes:
Ask your students if they see any practical advantage to this latch circuit over a gated latch built from NOR gates. What if they had to build a latch circuit from individual gates, rather than as a complete integrated circuit in and of itself? Would one design be preferable over the other?
Then, ask your students to compare the truth tables of the two different types of gated latches. Is there any difference in operation at all between the latch built with NAND gates and the latch built with NOR gates?

Question 13:

Here, a gated S-R latch is being used to control the electric power to a powerful ultraviolet lamp, used for sterilization of instruments in a laboratory environment:

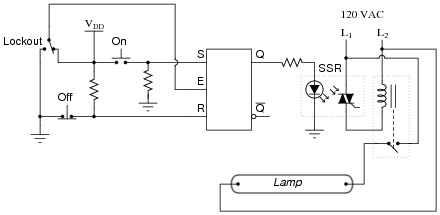
Based on your knowledge of how gated S-R latches function, what is the purpose of the "Lockout" switch? Also, explain how the CMOS latch is able to exert control over the high-power lamp (i.e. explain the operation of the interposing devices between the latch and the lamp).
Now, suppose the lab personnel want to add a feature to the ultraviolet sterilization chamber: an electric solenoid door lock, so that personnel can open the door to the chamber only if the following conditions are met:

�: Lamp is off
�: "Lockout" switch is sending a "low" signal to the latch's Enable input

Modify this circuit so that it energizes the door lock solenoid, allowing access to the chamber, only if the above conditions are both true.

The "Lockout" switch effectively disables the Ön" and Öff" controls when it sends a "low" signal to the latch's Enable input.
This circuit uses both a solid-state relay (SSR) and an electromechanical relay for interposing between the latch and the lamp. These devices allow the low-power latch circuit to exert control over the high-power lamp.
Here is one possibility for the door lock control:

Follow-up question: there are better (safer) ways to accomplish this same function. For instance, suppose the TRIAC inside the SSR were to fail shorted, maintaining power to the lamp even when the latch goes into the "reset" mode. Would the door-lock logic shown here prevent someone from opening the door and getting exposed to the strong ultraviolet light? Explain your answer!
Challenge question: why not just use one interposing device: either an SSR, or an electromagnetic relay? Why both types of devices in the same circuit?

Notes:
The purpose of the "Lockout" switch is fairly simple, and should be easy for the students to explain. On the other hand, the design and implementation of a door lock safety circuit is a more complex question, deserving of discussion because it involves several important and realistic considerations:

�: How do we go from a simple verbal description of logical conditions (lamp off, enable low) to an actual gate circuit?
�: What is the safest strategy to use in determining when it is safe to open the door?
�: How should the door lock logic interpose to the solenoid itself (this is not shown in the answer!)?
�: How would the principles of lock-out/tag-out apply to this system, if we were approaching the problem from the perspective of maintenance personnel rather than lab (operations) personnel?

The challenge question gets students thinking in terms of real-life currents and voltages, and the limitations of each device.

Question 14:

A variation on the gated S-R latch circuit is something called the D-latch:

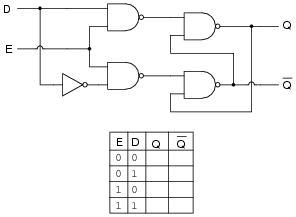
Complete the truth table for this D latch circuit, and identify which rows in the truth table represent the set, reset, and latch states, respectively.

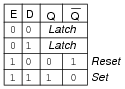
Notes:
Since this gate does not actually have "Set" and "Reset" inputs, ask your students to explain what conditions define the ßet" and "reset" states. Note that these state labels may be applied to any type of latch circuit.
To many of your students, this latch circuit may seem rather useless. Explain to them that this basic latch may be used to form memory cells, with each D latch storing 1 binary bit of information! Ask your students to explain, in their own words, how the latching action of this circuit constitutes a memory function. Under what condition(s) will the stored information in a D latch memory cell be lost?

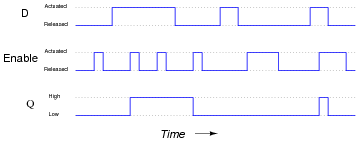
Question 15:

Complete the timing diagram, showing the state of the Q output over time as the input switches are actuated. Assume that Q begins in the low state on power-up:

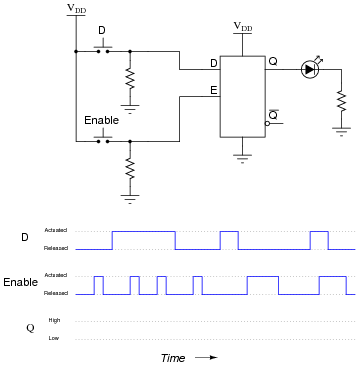
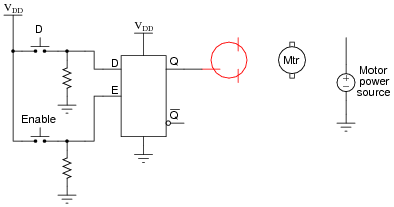
Follow-up question: complete a schematic diagram showing how this latch circuit could turn a motor on and off through a MOSFET.

Also, comment on whether your MOSFET sources current to the motor or sinks current from the motor.

Notes:
Some students may be confused about the width of the last pulse on the Q output. Remind them that Q follows D for as long as the Enable input is activated!

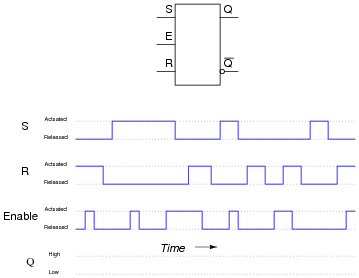
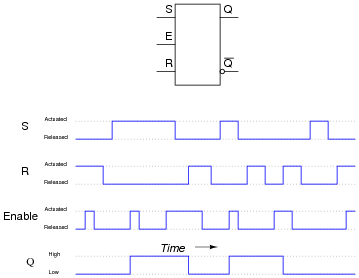
Question 16:

Complete the timing diagram, showing the state of the Q output over time as the input switches are actuated. Assume that Q begins in the low state on power-up:

Notes:
Have your students explain exactly how they arrived at the solution they did for the output waveform. Are they making use of a truth table for the S-R latch to figure out what happens? Are they doing it by memory? Can they discriminate between an output state change initiated by either the Set or Reset inputs versus one initiated by the enable going high?

Question 17:

An analog-to-digital converter is a circuit that inputs a variable (analog) voltage or current, and outputs multiple bits of binary data corresponding to the magnitude of that measured voltage or current. In the circuit shown here, an ADC inputs a voltage signal from a potentiometer, and outputs an 8-bit binary "word," which may then be read by a computer, transmitted digitally over a communications network, or stored on digital media:

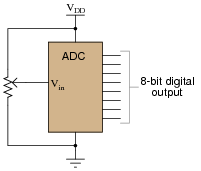
As the input voltage changes, the binary number output by the ADC will change as well. Suppose, though, that we want to have sample-and-hold capability added to this data acquisition circuit, to allow us to "freeze" the output of the ADC at will. Explain how using eight D latch circuits will give us this capability:

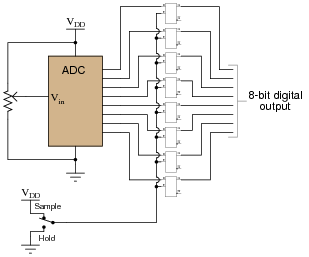
When the Sample/Hold switch is in the "low" position, the D latches all fall into the "latch" state, holding that last valid input states on their Q outputs.

Notes:
Sample-and-hold circuitry is quite common in modern data acquisition and other types of electronic systems. In this case, sample-and-hold showcases a practical use of D latch circuits. If your students have not yet heard of analog-to-digital converters, it might be a good idea to discuss some of their general principles. No knowledge of their internal workings is necessary in order to comprehend the circuit shown in the question, however.

Question 18:

Gated latch circuits often come packaged in multiple quantities, with common gate inputs, so that more than one of the latches within the integrated circuit will be enabled and disabled simultaneously. Examine this logic symbol, representative of the 74AC16373, a 16-bit D-type latch with tri-state outputs:

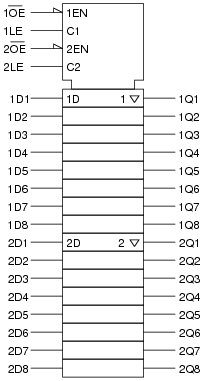
Note how the sixteen D latches are divided into two groups of eight. Explain the functions of the four inputs at the very top of the symbol (1EN, C1, 2EN, and C2). Which of these input lines correspond to the Ënable" inputs seen on single D-type latch circuits? Also, describe what the "wedge" shapes represent on the 1EN and 2EN input lines.
Suppose you wished to have all sixteen latch circuits enabled as one, rather than as two groups of eight. Show what you would have to do to this circuit in order to achieve this goal.

Inputs C1 and C2 perform the standard Ënabling" function for the D-type latches within this integrated circuit. The 1EN and 2EN inputs control the tri-state outputs. Their "wedge" symbols mean "complemented," and are equivalent to the "bubbles" seen on traditional gate symbols.
To make all sixteen latches enable and disable as one, bridge the enable inputs as such:

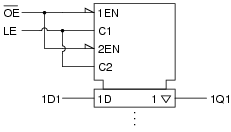
Notes:
This question not only introduces students to the concept of multiple latches in a single integrated circuit, but it also shows an example of IEEE/ANSI "block" symbolism. Your students, having become well adjusted to the idea of independent research by now, should have obtained the datasheet for this circuit (74AC16373) as part of their study. The information contained in the datasheet should prove to be quite informative in answering their questions about enable input functions, tri-state outputs, and the like. If they haven't obtained datasheets, and cannot understand the answers to the question(s), don't just tell them - have them look it up for themselves!

Question 19:

In many types of digital systems, a set of square-wave signals are phase-shifted from each other by 90^o. Such a phase relationship is called quadrature.
Determine the output of a D-type latch for this pair of quadrature signals, applied to the D and E inputs over time:

Then, determine the output of a D-type latch when the phase relationship is reversed, (D leading E by 90^o, instead of E leading D by 90^o):

Notes:
Students need to be proficient in analyzing pulse diagrams, especially with latch circuits (and later, with flip-flops), because these types of circuits often find application in pulse-driven systems.

Question 20:

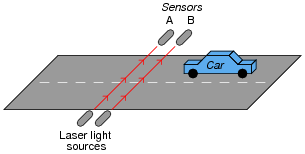
This one-way street is equipped with an alarm to signal drivers going the wrong way. The sensors work by light beams being broken when an automobile passes between them. The distance between the sensors is less than the length of a normal car, which means as a car passes by, first one beam is broken, then both beams become broken, then only the last beam is broken, then neither beam is broken. The sensors are phototransistors sensitive only to the narrow spectrum of light emitted by the laser light sources, so that ambient sunlight will not "fool" them:

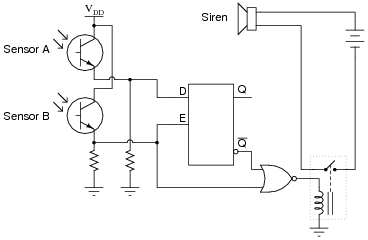
Both sensors connect to inputs on a D-type latch, which is then connected to some other circuitry to sound an alarm when a car goes down the road the wrong way:

The first question is this: which way is the correct way to drive down this street? From left to right, or from right to left (as shown in the illustration)?
The second question is, how will the system respond if sensor A's laser light source fails? What will happen if sensor B's laser light source fails?

Left-to-right is the correct driving direction for this street.
If sensor A's light source fails, the alarm will never activate. A failed light source for sensor B will have different effects on the system, depending on whether sensor A was sending a "high" or a "low" signal to the latch circuit at the time B's light source failed. I'll let you figure out which way triggers the alarm!

Notes:
This question is a great problem-solving exercise. Students must figure out how to set it up so that they may apply the rules of latch circuits and gate circuits, then they must analyze it correctly! Devote plenty of classroom time to a discussion of this problem.
Students may show a reluctance to draw a timing diagram when they approach this problem, even when they realize the utility of such a diagram. Instead, many will try to figure the circuit out just by looking at it. Note the emphasis on the word "try." This circuit is much more difficult to figure out without a timing diagram! Withhold your explanation of this circuit until each student shows you a timing diagram for it. Emphasize the fact that this step, although it consumes a bit of time, is actually a time-saver in the end.
It is easy as an instructor to focus so intently on teaching electronic theory that other practical matters become neglected. Electronic technicians and engineers do not simply work on circuits; they work on systems that happen to employ electronic circuits. Ultimately, nearly every electronic circuit they work with will have some relationship to the physical world. Problem solving exercises in school must include scenarios similar to real life, where conditions and functions other than electronics have a role in determining the solution. Only by exposing students to problems requiring them to think beyond pure electronics will they become adequately prepared to meet the challenges of their future careers.

Question 21:

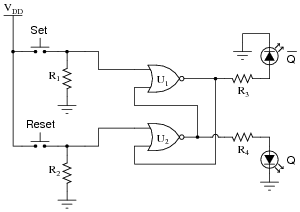
Identify at least one component fault that would cause the "[`Q]" LED to always remain off, no matter what was done with the input switches.

For each of your proposed faults, explain why it will cause the described problem.

�: Resistor R₃ failed open.
�: NOR gate U₁ output failed low.
�: Resistor R₁ failed open (provided enough ambient electrical noise to activate a floating gate input).
�: "Set" switch contacts failed shorted.

Notes:
Latch circuits can be confusing due to their use of positive feedback. Questions such as this are important tools for helping develop your students' understanding of latch circuits.

Question 22:

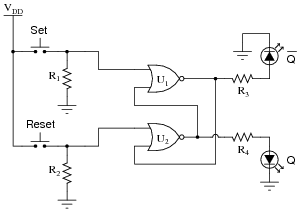
Identify at least one component fault that would cause the "Q" LED to always stay on, no matter what was done with the input switches.

For each of your proposed faults, explain why it will cause the described problem.

�: NOR gate U₂ output failed high.
�: Wire break between "Reset" switch and resistor R₂ (although if this was the only fault it may allow the Q LED to energize at power-up, just not de-energize after the "Set" button had been pressed).

Follow-up question: explain why the nature of the problem rules out the possibility of the only fault being something related to the feedback connections between U₁ and U₂.

Notes:
Latch circuits can be confusing due to their use of positive feedback. Questions such as this are important tools for helping develop your students' understanding of latch circuits.

Question 23:

A very common form of latch circuit is the simple ßtart-stop" relay circuit used for motor controls, whereby a pair of momentary-contact pushbutton switches control the operation of an electric motor. In this particular case, I show a low-voltage control circuit and a 3-phase, higher voltage motor:

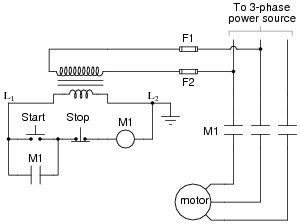
Explain the operation of this circuit, from the time the "Start" switch is actuated to the time the "Stop" switch is actuated. The normally-open M1 contact shown in the low-voltage control circuit is commonly called a seal-in contact. Explain what this contact does, and why it might be called a ßeal-in" contact.

Even though the "Start" and "Stop" switches are momentary, the ßeal-in" contact makes the circuit latch in one of two states: either motor energized or motor de-energized.

Notes:
Motor ßtart-stop" circuits are very common in industry, and apply to applications beyond electric motors. Ask your students if they can think of any application for a circuit such as this.

Question 24:

A student decides to build a motor start/stop control circuit based on the logic of a NOR gate S-R latch, rather than the usual simple ßeal-in" contact circuit:

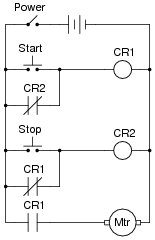
The circuit works fine, except that sometimes the motor starts all by itself when the circuit is first powered up! Other times, the motor remains off after power-up. In other words, the power-up state of this circuit is unpredictable.
Explain why this is so, and what might be done to prevent the motor from powering up in the "run" state.

What you have here is something called a race condition, where two or more relays "race" each other to attain mutually exclusive states. This is a difficult problem to fix, but the solution (and yes, there is more than one valid solution!) invariably involves "rigging" the race so that one of the relays is guaranteed to "win."

Notes:
Analyze the power-up states of this circuit with your students, and the "race" condition will become apparent. Such problems can be very difficult to locate and fix in real life, so it is good to expose students to them early in their education, and in contexts where the circuitry is not too confusing.

Question 25:

Don't just sit there! Build something!!

Learning to analyze relay circuits requires much study and practice. Typically, students practice by working through lots of sample problems and checking their answers against those provided by the textbook or the instructor. While this is good, there is a much better way.
You will learn much more by actually building and analyzing real circuits, letting your test equipment provide the änswers" instead of a book or another person. For successful circuit-building exercises, follow these steps:

1.: Draw the schematic diagram for the relay circuit to be analyzed.
2.: Carefully build this circuit on a breadboard or other convenient medium.
3.: Check the accuracy of the circuit's construction, following each wire to each connection point, and verifying these elements one-by-one on the diagram.
4.: Analyze the circuit, determining all logic states for given input conditions.
5.: Carefully measure those logic states, to verify the accuracy of your analysis.
6.: If there are any errors, carefully check your circuit's construction against the diagram, then carefully re-analyze the circuit and re-measure.

Always be sure that the power supply voltage levels are within specification for the relay coils you plan to use. I recommend using PC-board relays with coil voltages suitable for single-battery power (6 volt is good). Relay coils draw quite a bit more current than, say, semiconductor logic gates, so use a "lantern" size 6 volt battery for adequate operating life.
One way you can save time and reduce the possibility of error is to begin with a very simple circuit and incrementally add components to increase its complexity after each analysis, rather than building a whole new circuit for each practice problem. Another time-saving technique is to re-use the same components in a variety of different circuit configurations. This way, you won't have to measure any component's value more than once.

Let the electrons themselves give you the answers to your own "practice problems"!

Notes:
It has been my experience that students require much practice with circuit analysis to become proficient. To this end, instructors usually provide their students with lots of practice problems to work through, and provide answers for students to check their work against. While this approach makes students proficient in circuit theory, it fails to fully educate them.
Students don't just need mathematical practice. They also need real, hands-on practice building circuits and using test equipment. So, I suggest the following alternative approach: students should build their own "practice problems" with real components, and try to predict the various logic states. This way, the relay theory "comes alive," and students gain practical proficiency they wouldn't gain merely by solving Boolean equations or simplifying Karnaugh maps.
Another reason for following this method of practice is to teach students scientific method: the process of testing a hypothesis (in this case, logic state predictions) by performing a real experiment. Students will also develop real troubleshooting skills as they occasionally make circuit construction errors.
Spend a few moments of time with your class to review some of the "rules" for building circuits before they begin. Discuss these issues with your students in the same Socratic manner you would normally discuss the worksheet questions, rather than simply telling them what they should and should not do. I never cease to be amazed at how poorly students grasp instructions when presented in a typical lecture (instructor monologue) format!
A note to those instructors who may complain about the "wasted" time required to have students build real circuits instead of just mathematically analyzing theoretical circuits:
What is the purpose of students taking your course?
If your students will be working with real circuits, then they should learn on real circuits whenever possible. If your goal is to educate theoretical physicists, then stick with abstract analysis, by all means! But most of us plan for our students to do something in the real world with the education we give them. The "wasted" time spent building real circuits will pay huge dividends when it comes time for them to apply their knowledge to practical problems.
Furthermore, having students build their own practice problems teaches them how to perform primary research, thus empowering them to continue their electrical/electronics education autonomously.
In most sciences, realistic experiments are much more difficult and expensive to set up than electrical circuits. Nuclear physics, biology, geology, and chemistry professors would just love to be able to have their students apply advanced mathematics to real experiments posing no safety hazard and costing less than a textbook. They can't, but you can. Exploit the convenience inherent to your science, and get those students of yours practicing their math on lots of real circuits!

Question 26:

Latch circuits such as the S-R latch and the D latch are often referred to as transparent digital devices. Explain what this term means, and why latches are classified as such.

A "transparent" digital device is one whose outputs immediately and asynchronously (transparently) follow the input signal(s) when enabled. By contrast, many other digital devices are synchronous, meaning their outputs follow the inputs only at specified times (at the command of a "clock" signal).

Notes:
The term "transparent" becomes more meaningful when latches and flip-flops are compared with one another.