Logarithms for analog circuits : Worksheet

The concept of a mathematical power is familiar to most students of algebra. For instance, ten to the third power means this:

10³ = 10 ×10 ×10 = 1000

. . . and eight to the seventh power means this:

8⁷ = 8 ×8 ×8 ×8 ×8 ×8 ×8 = 2,097,152

Just as subtraction is the inverse function of addition, and division is the inverse function of multiplication (because with inverse functions, one ündoes" the other), there is also an inverse function for a power and we call it the logarithm.
Re-write the expression 10³ = 1000 so that it uses the same quantities (10, 3, and 1000) in the context of a logarithm instead of a power, just as the subtraction is shown here to be the inverse of addition, and division is shown to be the inverse of multiplication in the following examples:

3 + 8 = 11 (+ and - are inverse functions) 11 - 3 = 8

2 ×7 = 14 (× and �are inverse functions) 14 �2 = 7

10³ = 1000 (powers and logs are inverse functions) log₁₀ ??? = ???

Reveal Answer

10³ = 1000 (powers and logs are inverse functions) log₁₀ 1000 = 3

Notes:
In my experience, most American students are woefully underprepared for the subject of logarithms when they study with me. Admittedly, logarithms do not see as much use in everyday life as powers do (and that is very little for most people as it is!). Logarithms used to be common fare for secondary school and college students, as they were essential for the operation of a slide rule, an elegant mechanical analog computing device popular decades ago.
The purpose of this question is to twofold: to get students to realize what a logarithm is, and also to remind them of the concept of inverse functions, which become very important in analog computational circuits.

Hide Answer

Given the following mathematical expression, write another one defining a logarithm using the same variables:

If: x^y = z Then: log_? ? = ?

Reveal Answer

If: x^y = z Then: log_x z = y

Notes:
Nothing special here. Indeed, the answer to this question may be derived from any algebra textbook.

Hide Answer

Electronic calculators with logarithm capability have at least two different types of logarithms: common logarithm and natural logarithm, symbolized as "log" and "ln", respectively. Explain what the difference is between these two types of logarithms.

Reveal Answer

The common logarithm function assumes a "base" value of ten, whereas the natural logarithm assumes a base value of e (Euler's constant).
Follow-up question: what is the approximate value of e? How can you get your calculator to give you the answer (rather than looking it up in a math book?

Notes:
Some calculators, of course, allow you to extract the logarithm of any number to any base. Here, I simply want students to become familiar with the two logarithm functions available on the most basic scientific calculators.
Note that some calculators will show just enough digits of e to give the false impression that they repeat (ten digits: e = 2.718281828). If anyone suggests that e is a (rational) repeating decimal number, correct this misunderstanding by telling them it is irrational just like p.

Hide Answer

Note the following logarithmic identities, using the "common" (base 10) logarithm:

log10 = 1

log100 = 2

log1000 = 3

log10000 = 4

In the first equation, the numbers 10 and 1 were related together by the log function. In the second equation, the numbers 100 and 2 were related together by the same log function, and so on.
Rewrite the four equations together in such a way that the same numbers are related to each other, but without writing "log". In other words, represent the same mathematical relationships using some mathematical function other than the common logarithm function.

Reveal Answer

10¹ = 10

10² = 100

10³ = 1000

10⁴ = 10000

Notes:
An illustration like this helps students comprehend what the "log" function actually does.

Hide Answer

Note the following logarithmic identities, using the "common" (base 10) logarithm:

log0.1 = -1

log0.01 = -2

log0.001 = -3

log0.0001 = -4

In the first equation, the numbers 0.1 and 1 were related together by the log function. In the second equation, the numbers 0.01 and 2 were related together by the same log function, and so on.
Rewrite the four equations together in such a way that the same numbers are related to each other, but without writing "log". In other words, represent the same mathematical relationships using some mathematical function other than the common logarithm function.

Reveal Answer

10^-1 = 0.1

10^-2 = 0.01

10^-3 = 0.001

10^-4 = 0.0001

Notes:
An illustration like this helps students comprehend what the "log" function actually does.

Hide Answer

Examine the following progression of mathematical statements:

(10²)(10³) = 100000

10²⁺³ = 100000

10⁵ = 100000

What does this pattern indicate? What principle of algebra is illustrated by these three equations?
Next, examine this progression of mathematical statements:

log10⁵ = log100000 = 5

log10²⁺³ = log100000 = 5

log10² + log10³ = log100000 = 5

What does this pattern indicate? What principle of algebra is illustrated by these three equations?

Reveal Answer

First pattern:
The product of two base numbers with different exponents is equal to that base number raised to the power of the exponents' sum.
Second pattern:
The sum of two logarithms is equal to the logarithm of those two numbers' product.

Notes:
In this question, I want students to begin to see how logarithms relate multiplication to addition, and how powers relate addition to multiplication. This is an initial step to students recognizing logarithms as transform functions: a means to transform one type of mathematical problem into a simpler type of mathematical problem.

Hide Answer

Examine this progression of mathematical statements:

(100)(1000) = 100000

(100)(1000) = 10⁵

log[(100)(1000)] = log10⁵

log100 + log1000 = log10⁵

log10² + log10³ = log10⁵

2 + 3 = 5

What began as a multiplication problem ended up as an addition problem, through the application of logarithms. What does this tell you about the utility of logarithms as an arithmetic tool?

Reveal Answer

That logarithms can reduce the complexity of an equation from multiplication, down to addition, indicates its usefulness as a tool to simplify arithmetic problems. Specifically, the logarithm of a product is equal to the sum of the logarithms of the two numbers being multiplied.

Notes:
In mathematics, any procedure that reduces a complex type of problem into a simpler type of problem is called a transform function, and logarithms are one of the simplest types of transform functions in existence.

Hide Answer

Suppose you owned a scientific calculator with two broken buttons: the multiply (×) and divide (�). Demonstrate how you could solve this simple multiplication problem using only logarithms, addition, and antilogarithms (powers):

7 ×5 = ???

The answer to this problem was easy enough for you to figure out without a calculator at all, so here are some more practice problems for you to try:

�: 23 ×35 =
�: 781 ×92 =
�: 19.4 ×60 =
�: 0.019 ×2.6 =

Reveal Answer

Here I will show you the steps to using logarithms to solve the first multiplication problem:

7 ×5 = ???

7 ×5 = 10^{log7 + log5}

7 ×5 = 10^{0.8451 + 0.6990}

7 ×5 = 10^1.5441

7 ×5 = 35

Since the others are easy enough for you to check (with your non-broken calculator!), I'll leave their solutions in your capable hands.

Notes:
Incidentally, there is nothing special about the common logarithm to warrant its exclusive use in this problem. We could have just as easily applied the natural logarithm function with the same (final) result:

7 ×5 = ???

7 ×5 = e^{ln7 + ln5}

7 ×5 = e^{1.9459 + 1.6094}

7 ×5 = e^3.5553

7 ×5 = 35

Hide Answer

Examine this progression of mathematical statements:

1000

100

= 10

1000

100

= 10¹

log

�
�

1000

100

�
�

= log10¹

log1000 - log100 = log10¹

log10³ - log10² = log10¹

3 - 2 = 1

What began as a division problem ended up as a subtraction problem, through the application of logarithms. What does this tell you about the utility of logarithms as an arithmetic tool?

Reveal Answer

That logarithms can reduce the complexity of an equation from division, down to subtraction, indicates its usefulness as a tool to simplify arithmetic problems. Specifically, the logarithm of a quotient is equal to the difference between the logarithms of the two numbers being divided.

Notes:
In mathematics, any procedure that reduces a complex type of problem into a simpler type of problem is called a transform function, and logarithms are one of the simplest types of transform functions in existence.

Hide Answer

Suppose you owned a scientific calculator with two broken buttons: the multiply (×) and divide (�). Demonstrate how you could solve this simple multiplication problem using only logarithms, addition, and antilogarithms (powers):

12 �3 = ???

The answer to this problem was easy enough for you to figure out without a calculator at all, so here are some more practice problems for you to try:

�: 122 �35 =
�: 781 �92 =
�: 19.4 �60 =
�: 3.5 �0.21 =

Reveal Answer

Here I will show you the steps to using logarithms to solve the first multiplication problem:

12 �3 = ???

12 �3 = 10^{log12 - log3}

12 �3 = 10^{1.0792 - 0.4771}

12 �3 = 10^0.6021

12 �3 = 4

Since the others are easy enough for you to check (with your non-broken calculator!), I'll leave their solutions in your capable hands.

Notes:
Incidentally, there is nothing special about the common logarithm to warrant its exclusive use in this problem. We could have just as easily applied the natural logarithm function with the same (final) result:

12 �3 = ???

12 �3 = e^{ln12 - ln3}

12 �3 = e^{2.4849 - 1.0986}

12 �3 = e^1.3863

12 �3 = 4

Hide Answer

Examine this progression of mathematical statements:

(1000)² = 1000000

(1000)² = 10⁶

log[(1000)²] = log10⁶

(2)(log1000) = log10⁶

(2)(log10³) = log10⁶

(2)(3) = 6

What began as an exponential problem ended up as a multiplication problem, through the application of logarithms. What does this tell you about the utility of logarithms as an arithmetic tool?

Reveal Answer

That logarithms can reduce the complexity of an equation from exponentiation, down to multiplication, indicates its usefulness as a tool to simplify arithmetic problems. Specifically, the logarithm of a number raised to a power is equal to that power multiplied by the logarithm of the number.

Notes:
In mathematics, any procedure that reduces a complex type of problem into a simpler type of problem is called a transform function, and logarithms are one of the simplest types of transform functions in existence.

Hide Answer

Suppose you owned a scientific calculator with two broken buttons: the power (y^x) and root (^x�{y}). Demonstrate how you could solve this simple power problem using only logarithms, multiplication, and antilogarithms (powers):

3⁴ = ???

The answer to this problem was easy enough for you to figure out without a calculator at all, so here are some more practice problems for you to try:

�: 25⁶ =
�: 564³ =
�: 0.224² =
�: 41^0.3 =

Reveal Answer

Here I will show you the steps to using logarithms to solve the first multiplication problem:

3⁴ = ???

3⁴ = 10^{(4 log3)}

3⁴ = 10^(4)(0.4771)

3⁴ = 10^1.9085

3⁴ = 81

Since the others are easy enough for you to check (with your non-broken calculator!), I'll leave their solutions in your capable hands.

Notes:
Incidentally, there is nothing special about the common logarithm to warrant its exclusive use in this problem. We could have just as easily applied the natural logarithm function with the same (final) result:

3⁴ = ???

3⁴ = e^{(4 ln3)}

3⁴ = e^(4)(1.0986)

3⁴ = e^4.3944

3⁴ = 81

Hide Answer

Examine this progression of mathematical statements:

�

1000

= 10^1.5

log

�

1000

= log( 10^1.5 )

log( 1000^¹/₂ ) = log( 10^1.5 )

1

2

(log1000) = log( 10^1.5 )

1

2

(log10³) = log( 10^1.5 )

3

2

(log10) = log( 10^1.5 )

3

2

(1) = log( 10^1.5 )

3

2

= log( 10^1.5 )

3

2

= 1.5

What began as a fractional exponent problem ended up as a simple fraction, through the application of logarithms. What does this tell you about the utility of logarithms as an arithmetic tool?

Reveal Answer

That logarithms can reduce the complexity of an equation from fractional exponentiation, down to simple fractions, indicates its usefulness as a tool to simplify arithmetic problems. Specifically, the logarithm of a root of a number is equal to the logarithm of that number divided by the root index.

Notes:
In mathematics, any procedure that reduces a complex type of problem into a simpler type of problem is called a transform function, and logarithms are one of the simplest types of transform functions in existence.

Hide Answer

Suppose you owned a scientific calculator with two broken buttons: the power (y^x) and root (^x�{y}). Demonstrate how you could solve this simple root problem using only logarithms, division, and antilogarithms (powers):

3

�

8

= ???

The answer to this problem was easy enough for you to figure out without a calculator at all, so here are some more practice problems for you to try:

�: ⁴�{13} =
�: ⁵�{209} =
�: ^2.5�{9935} =
�: ^9.2�{0.15} =

Reveal Answer

Here I will show you the steps to using logarithms to solve the first multiplication problem:

3

�

8

= ???

3

�

8

= 10^{( ¹/₃ log8 )}

3

�

8

= 10^{( ¹/₃ (0.9031) )}

3

�

8

= 10^0.3010

3

�

8

= 2

Since the others are easy enough for you to check (with your non-broken calculator!), I'll leave their solutions in your capable hands.

Notes:
Incidentally, there is nothing special about the common logarithm to warrant its exclusive use in this problem. We could have just as easily applied the natural logarithm function with the same (final) result:

3

�

8

= ???

3

�

8

= e^{( ¹/₃ ln8 )}

3

�

8

= e^{( ¹/₃ (2.0794) )}

3

�

8

= e^0.6931

3

�

8

= 2

Hide Answer

You may be wondering why anyone would bother using logarithms to solve arithmetic problems for which we have perfectly good and effective digital electronic calculator functions at our disposal. For example, why would anyone do this:

10^{log7 + log5}

. . . when they could just do the following on the same calculator?

7 ×5

The quick answer to this very good question is, "when it is more difficult to directly multiply two numbers." The trouble is, most people have a difficult time imagining when it would ever be easier to take two logarithms, add them together, and raise ten to that power than it would be to simply multiply the original two numbers together.
The answer to that mystery is found in operational amplifier circuitry. As it turns out, it is much easier to build single opamp circuits that add, subtract, exponentiate, or take logarithms than it is to build one that directly multiplies or divides two quantities (analog voltages) together.
We may think of these opamp functions as "blocks" which may be interconnected to perform composite arithmetic functions:

Using this model of specific math-function "blocks," show how the following set of analog math function blocks may be connected together to multiply two analog voltages together:

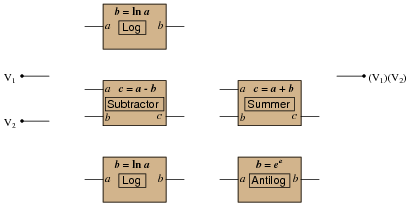
Reveal Answer

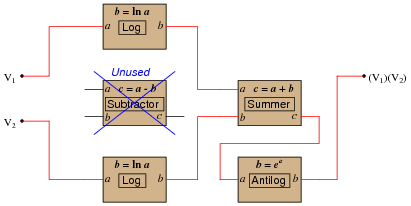
Notes:
The purpose of this question is simple: to provide a practical application for logarithms as computational aids in an age of cheap, ubiquitous, digital computing devices.

Hide Answer

Logarithms have interesting properties, which we may exploit in electronic circuits to perform certain complex operations. In this question, I recommend you use a hand calculator to explore these properties.
Calculate the following:

�: 10^log3 =
�: log(10⁸) =

�: e^ln3 =
�: ln(e⁸) =

�: 10^{(log3 + log5)} =
�: e^{(ln3 + ln5)} =

�: 10^{(log2.2 + log4)} =
�: e^{(ln2.2 + ln4)} =

�: 10^{(log12 - log4)} =
�: e^{(ln12 - ln4)} =

�: 10^{(2 log3)} =
�: e^{(2 ln3)} =

�: 10^([log25/2]) =
�: e^([ln25/2]) =

Reveal Answer

�: 10^log3 = 3
�: log(10⁸) = 8

�: e^ln3 = 3
�: ln(e⁸) = 8

�: 10^{(log3 + log5)} = 15
�: e^{(ln3 + ln5)} = 15

�: 10^{(log2.2 + log4)} = 8.8
�: e^{(ln2.2 + ln4)} = 8.8

�: 10^{(log12 - log4)} = 3
�: e^{(ln12 - ln4)} = 3

�: 10^{(2 log3)} = 9
�: e^{(2 ln3)} = 9

�: 10^([log25/2]) = 5
�: e^([ln25/2]) = 5

Notes:
Discuss what mathematical operations are being done with the constants in these equations, by using logarithms. What patterns do your students notice? Also, discuss the terms "log" and äntilog," and relate them to opamp circuits they've seen.
Ask your students whether or not they think it matters what "base" of logarithm is used in these equations. Can they think of any other arithmetic operations to try using logarithms in this manner?

Hide Answer

Learning Electronics

Logarithms for analog circuits

Question 1:

Question 2:

Question 3:

Question 4:

Question 5:

Question 6:

Question 7:

Question 8:

Question 9:

Question 10:

Question 11:

Question 12:

Question 13:

Question 14:

Question 15:

Question 16: