Resonance
Question 1:
The Q factor of a series inductive circuit is given by the following equation:
|
Likewise, we know that inductive reactance may be found by the following equation:
|
We also know that the resonant frequency of a series LC circuit is given by this equation:
|
Through algebraic substitution, write an equation that gives the Q factor of a series resonant LC circuit exclusively in terms of L, C, and R, without reference to reactance (X) or frequency (f).
|
Notes:
This is merely an exercise in algebra. However, knowing how these three component values affects the Q factor of a resonant circuit is a valuable and practical insight!
Question 2:
| Don't just sit there! Build something!! |
Learning to mathematically analyze circuits requires much study and practice. Typically, students practice by working through lots of sample problems and checking their answers against those provided by the textbook or the instructor. While this is good, there is a much better way.
You will learn much more by actually building and analyzing real circuits, letting your test equipment provide the änswers" instead of a book or another person. For successful circuit-building exercises, follow these steps:
- 1.
- Carefully measure and record all component values prior to circuit construction.
- 2.
- Draw the schematic diagram for the circuit to be analyzed.
- 3.
- Carefully build this circuit on a breadboard or other convenient medium.
- 4.
- Check the accuracy of the circuit's construction, following each wire to each connection point, and verifying these elements one-by-one on the diagram.
- 5.
- Mathematically analyze the circuit, solving for all voltage and current values.
- 6.
- Carefully measure all voltages and currents, to verify the accuracy of your analysis.
- 7.
- If there are any substantial errors (greater than a few percent), carefully check your circuit's construction against the diagram, then carefully re-calculate the values and re-measure.
For AC circuits where inductive and capacitive reactances (impedances) are a significant element in the calculations, I recommend high quality (high-Q) inductors and capacitors, and powering your circuit with low frequency voltage (power-line frequency works well) to minimize parasitic effects. If you are on a restricted budget, I have found that inexpensive electronic musical keyboards serve well as "function generators" for producing a wide range of audio-frequency AC signals. Be sure to choose a keyboard "voice" that closely mimics a sine wave (the "panflute" voice is typically good), if sinusoidal waveforms are an important assumption in your calculations.
As usual, avoid very high and very low resistor values, to avoid measurement errors caused by meter "loading". I recommend resistor values between 1 kW and 100 kW.
One way you can save time and reduce the possibility of error is to begin with a very simple circuit and incrementally add components to increase its complexity after each analysis, rather than building a whole new circuit for each practice problem. Another time-saving technique is to re-use the same components in a variety of different circuit configurations. This way, you won't have to measure any component's value more than once.
Notes:
It has been my experience that students require much practice with circuit analysis to become proficient. To this end, instructors usually provide their students with lots of practice problems to work through, and provide answers for students to check their work against. While this approach makes students proficient in circuit theory, it fails to fully educate them.
Students don't just need mathematical practice. They also need real, hands-on practice building circuits and using test equipment. So, I suggest the following alternative approach: students should build their own "practice problems" with real components, and try to mathematically predict the various voltage and current values. This way, the mathematical theory "comes alive," and students gain practical proficiency they wouldn't gain merely by solving equations.
Another reason for following this method of practice is to teach students scientific method: the process of testing a hypothesis (in this case, mathematical predictions) by performing a real experiment. Students will also develop real troubleshooting skills as they occasionally make circuit construction errors.
Spend a few moments of time with your class to review some of the "rules" for building circuits before they begin. Discuss these issues with your students in the same Socratic manner you would normally discuss the worksheet questions, rather than simply telling them what they should and should not do. I never cease to be amazed at how poorly students grasp instructions when presented in a typical lecture (instructor monologue) format!
An excellent way to introduce students to the mathematical analysis of real circuits is to have them first determine component values (L and C) from measurements of AC voltage and current. The simplest circuit, of course, is a single component connected to a power source! Not only will this teach students how to set up AC circuits properly and safely, but it will also teach them how to measure capacitance and inductance without specialized test equipment.
A note on reactive components: use high-quality capacitors and inductors, and try to use low frequencies for the power supply. Small step-down power transformers work well for inductors (at least two inductors in one package!), so long as the voltage applied to any transformer winding is less than that transformer's rated voltage for that winding (in order to avoid saturation of the core).
A note to those instructors who may complain about the "wasted" time required to have students build real circuits instead of just mathematically analyzing theoretical circuits:
What is the purpose of students taking your course?
If your students will be working with real circuits, then they should learn on real circuits whenever possible. If your goal is to educate theoretical physicists, then stick with abstract analysis, by all means! But most of us plan for our students to do something in the real world with the education we give them. The "wasted" time spent building real circuits will pay huge dividends when it comes time for them to apply their knowledge to practical problems.
Furthermore, having students build their own practice problems teaches them how to perform primary research, thus empowering them to continue their electrical/electronics education autonomously.
In most sciences, realistic experiments are much more difficult and expensive to set up than electrical circuits. Nuclear physics, biology, geology, and chemistry professors would just love to be able to have their students apply advanced mathematics to real experiments posing no safety hazard and costing less than a textbook. They can't, but you can. Exploit the convenience inherent to your science, and get those students of yours practicing their math on lots of real circuits!
Question 3:
Not only do reactive components unavoidably possess some parasitic (ßtray") resistance, but they also exhibit parasitic reactance of the opposite kind. For instance, inductors are bound to have a small amount of capacitance built-in, and capacitors are bound to have a small amount of inductance built-in. These effects are not intentional, but they exist anyway.
Describe how a small amount of capacitance comes to exist within an inductor, and how a small amount of inductance comes to exist within a capacitor. Explain what it is about the construction of these two reactive components that allows the existence of öpposite" characteristics.
Notes:
Once students have identified the mechanisms of parasitic reactances, challenge them with inventing means of minimizing these effects. This is an especially practical exercise for understanding parasitic inductance in capacitors, which is very undesirable in decoupling capacitors used to stabilize power supply voltages near integrated circuit "chips" on printed circuit boards. Fortunately, most of the stray inductance in a decoupling capacitor is due to how it's mounted to the board, rather than anything within the structure of the capacitor itself.
Question 4:
Calculate the resonant frequency of this parallel LC circuit, and qualitatively describe its total impedance (Ztotal) when operating at resonance:
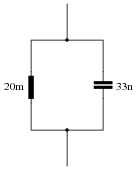
|
|
Ztotal @ fr = �
Notes:
Nothing special to note here, just an application of the resonance formula and a review of parallel LC resonance.
Question 5:
If a metal bar is struck against a hard surface, the bar will "ring" with a characteristic frequency. This is the fundamental principle upon which tuning forks work:

|
|
The ability of any physical object to "ring" like this after being struck is dependent upon two complementary properties: mass and elasticity. An object must possess both mass and a certain amount of ßpringiness" in order to physically resonate.
Describe what would happen to the resonant frequency of a metal bar if it were made of a more elastic (less ßtiff") metal? What would happen to the resonant frequency if an extra amount of mass were added to the end being struck?
Notes:
Electrical resonance is so closely related to physical resonance, that I believe questions like this help students grasp the concept better. Everyone knows what resonance is in the context of a vibrating object (tuning fork, bell, wind chime, guitar string, cymbal head), even if they have never heard of the term "resonance" before. Getting them to understand that mechanical resonance depends on the complementary qualities of mass and elasticity primes their minds for understanding that electrical resonance depends on the complementary qualities of inductance and capacitance.
Question 6:
This simple electric circuit is capable of resonance, whereby voltage and current oscillate at a frequency characteristic to the circuit:
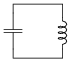
|
|
In a mechanical resonant system - such as a tuning fork, a bell, or a guitar string - resonance occurs because the complementary properties of mass and elasticity exchange energy back and forth between each other in kinetic and potential forms, respectively. Explain how energy is stored and transferred back and forth between the capacitor and inductor in the resonant circuit shown in the illustration, and identify which of these components stores energy in kinetic form, and which stores energy in potential form.
Notes:
Ask your students to define "potential" and "kinetic" energy. These terms, of course, are central to the question, and I have not bothered to define them. This omission is purposeful, and it is the students' responsibility to research the definitions of these words in the process of answering the question. If a substantial number of your students stopped trying to answer the question when they encountered new words (instead of taking initiative to find out what the words mean), then it indicates a need to focus on independent learning skills (and attitudes!).
Discuss a typical "cycle" of energy exchange between kinetic and potential forms in a vibrating object, and then relate this exchange process to the oscillations of a tank circuit (capacitor and inductor).
Question 7:
Resonant electric circuits are analogous to resonant mechanical systems. They both oscillate, and their oscillation is founded on an exchange of energy between two different forms.
Mechanical engineers studying vibrations in machinery sometimes use capacitors and inductors to model the physical characteristics of mechanical systems. Specifically, capacitors model elasticity, while inductors model mass.
Explain what mechanical quantities in a resonant system are analogous to voltage and current in a resonant circuit.
Challenge question: specifically relate voltage and current for an inductor to force and velocity for a mass, and voltage and current for a capacitor to force and velocity for a spring. Illustrate the similarities mathematically, where possible!
Notes:
This is a challenging question, and it is one I would reserve for students destined to become engineers. However, once answered, it brings deep insight to the phenomenon of resonance both mechanical and electrical.
Question 8:
If an oscilloscope is set up for ßingle-sweep" triggering and connected to a DC-excited resonant circuit such as the one shown in the following schematic, the resulting oscillation will last just a short time (after momentarily pressing and releasing the pushbutton switch):
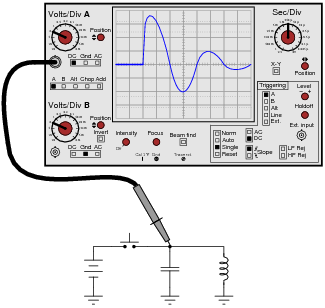
|
|
Explain why the oscillations die out, rather than go on forever. Hint: the answer is fundamentally the same as why a swinging pendulum eventually comes to a stop.
Notes:
A circuit such as this is easy to build and demonstrate, but you will need a digital storage oscilloscope to successfully capture the damped oscillations. Also, the results may be tainted by switch "bounce," so be prepared to address that concept if you plan to demonstrate this to a live audience.
You might want to ask your students how they would suggest building a "tank circuit" that is as free from energy losses as possible. If a perfect tank circuit could be built, how would it act if momentarily energized by a DC source such as in this setup?
Question 9:
How may the resonant frequency of this tank circuit be increased?
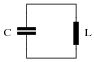
|
|
Note: this is not the only way to increase this circuit's resonant frequency!
Notes:
Challenge your students to explain another method for increasing the resonant frequency of this tank circuit, besides decreasing the value of the capacitor. Discuss how any of these alterations to the circuit affect the typical energy "cycle" between kinetic and potential forms, and why they lead to an increased frequency.
Question 10:
Very interesting things happen to resonant systems when they are ëxcited" by external sources of oscillation. For example, a pendulum is a simple example of a mechanically resonant system, and we all know from experience with swings in elementary school that we can make a pendulum achieve very high amplitudes of oscillation if we öscillate" our legs at just the right times to match the swing's natural (resonant) frequency.
Identify an example of a mechanically resonant system that is ëxcited" by an external source of oscillations near its resonant frequency. Hint: research the word "resonance" in engineering textbooks, and you are sure to read about some dramatic examples of resonance in action.
Challenge question: after researching the behavior of mechanical resonant systems when driven by external oscillations of the same frequency, determine what the effects might be of external oscillations on an electrical resonant system.
Notes:
Many, many examples of mechanical resonance exist, some of which are quite dramatic. A famous example of destructive mechanical resonance (of a well-known bridge in Washington state) has been immortalized in video form, and is easily available on the internet. If possible, provide the means within your classroom to display a video clip on computer, for any of the students who happen to find this video file and bring it to discussion.
Question 11:
If a capacitor and an inductor are connected in series, and energized by an AC voltage source with such a frequency that the reactances of each component are 125 W and 170 W, respectively, what is the total impedance of the series combination?
Now, of course, you are wondering: "how can two series-connected components have a total impedance that is less than either of their individual impedances?" Don't series impedances add to equal the total impedance, just like series resistances? Be prepared to explain what is happening in this circuit, during discussion time with your classmates.
Notes:
This question is an exercise in complex number arithmetic, and it is quite counter-intuitive at first. Discuss this problem in depth with your students, so that they are sure to comprehend the phenomenon of series-canceling impedances.
Question 12:
Calculate all voltage drops and current in this LC circuit at each of the given frequencies:
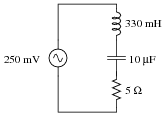
|
|
-
Frequency VL VC Itotal
50 Hz
60 Hz
70 Hz
80 Hz
90 Hz
100 Hz
Also, calculate the resonant frequency of this circuit.
-
Frequency VL VC Itotal
50 Hz 0.121 V 0.371 V 1.16 mA
60 Hz 0.221 V 0.471 V 1.77 mA
70 Hz 0.440 V 0.690 V 3.03 mA
80 Hz 1.24 V 1.49 V 7.48 mA
90 Hz 4.25 V 4.03 V 22.8 mA
100 Hz 1.07 V 0.821 V 5.16 mA
|
Notes:
This is nothing more than number-crunching, though some students may have found novel ways to speed up their calculations or verify their work.
Question 13:
Suppose we were to build a series "LC" circuit and connect it to a function generator, where we could vary the frequency of the AC voltage powering it:
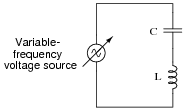
|
|
Calculate the amount of current in the circuit, given the following figures:
- �
- Power supply voltage = 3 volts RMS
- �
- Power supply frequency = 100 Hz
- �
- Capacitor = 4.7 mF
- �
- Inductor = 100 mH
Then, describe what happens to the circuit current as the frequency is gradually increased.
Follow-up question: what do you suppose might happen to the circuit current if the frequency is increased to the point that the reactances of the inductor and capacitor completely cancel each other? What safety concerns might arise from this possibility?
Notes:
In order for your students to arrive at the answer of circuit current increasing with frequency, they must perform a few calculations at different frequencies. Do this together, as a group, and note how the circuit's impedance changes with frequency.
Question 14:
Calculate the power supply frequency at which the reactances of a 33 mF and a 75 mH inductor are exactly equal to each other. Derive a mathematical equation from the individual reactance equations (XL = 2 pf L and XC = [1/(2 pf C)]), solving for frequency (f) in terms of L and C in this condition.
Calculate the total impedance of these two components, if they were connected in series, at that frequency.
Notes:
The answer gives away the meaning of this question: the determination of an LC circuit's resonant frequency. Students may be surprised at the total impedance figure of 0 W, but this is really nothing more than an extension of the ïmpedance cancellation" concept they've seen before in other series LC circuit questions. In this case, the cancellation concept has merely been taken to the ultimate level of total cancellation between the two impedances.
Question 15:
Calculate all voltages and currents in this circuit, at a power supply frequency near resonance:
|
|
Based on your calculations, what general predictions can you make about series-resonant circuits, in terms of their total impedance, their total current, and their individual component voltage drops?
Follow-up question: suppose the capacitor were to fail shorted. Identify how this failure would alter the circuit's current and voltage drops.
Notes:
This question is given without a specified source frequency for a very important reason: to encourage students to ëxperiment" with numbers and explore concepts on their own. Sure, I could have given a power supply frequency as well, but I chose not to because I wanted students to set up part of the problem themselves.
In my experience teaching, students will often choose to remain passive with regard to a concept they do not understand, rather than aggressively pursue an understanding of it. They would rather wait and see if the instructor happens to cover that concept during class time than take initiative to explore it on their own. Passivity is a recipe for failure in life, and this includes intellectual endeavors as much as anything else. The fundamental trait of autonomous learning is the habit of pursuing the answer to a question, without being led to do so. Questions like this, which purposefully omit information, and thus force the student to think creatively and independently, teach them to develop this trait.
Question 16:
Calculate all voltages and currents in this circuit, at a power supply frequency near resonance:
|
|
Based on your calculations, what general predictions can you make about parallel-resonant circuits, in terms of their total impedance, their total current, and their individual component currents?
Follow-up question: suppose the inductor were to fail open. Identify how this failure would alter the circuit's current and voltage drops.
Notes:
This question is given without a specified source frequency for a very important reason: to encourage students to ëxperiment" with numbers and explore concepts on their own. Sure, I could have given a power supply frequency as well, but I chose not to because I wanted students to set up part of the problem themselves.
In my experience teaching, students will often choose to remain passive with regard to a concept they do not understand, rather than aggressively pursue an understanding of it. They would rather wait and see if the instructor happens to cover that concept during class time than take initiative to explore it on their own. Passivity is a recipe for failure in life, and this includes intellectual endeavors as much as anything else. The fundamental trait of autonomous learning is the habit of pursuing the answer to a question, without being led to do so. Questions like this, which purposefully omit information, and thus force the student to think creatively and independently, teach them to develop this trait.
Question 17:
Does a series LC circuit äppear" capacitive or inductive (from the perspective of the AC source powering it) when the source frequency is greater than the circuit's resonant frequency? What about a parallel resonant circuit? In each case, explain why.
Notes:
Ask your students to explain their answers mathematically.
Question 18:
A paradoxical property of resonant circuits is that they have the ability to produce quantities of voltage or current (in series and parallel circuits, respectively) exceeding that output by the power source itself. This is due to the cancellation of inductive and capacitive reactances at resonance.
Not all resonant circuits are equally effective in this regard. One way to quantify the performance of resonant circuits is to assign them a quality factor, or Q rating. This rating is very similar to the one given inductors as a measure of their reactive "purity."
Suppose we have a resonant circuit operating at its resonant frequency. How may we calculate the Q of this operating circuit, based on empirical measurements of voltage or current? There are two answers to this question: one for series circuits and one for parallel circuits.
|
|
Follow-up question: what unique safety hazards may high-Q resonant circuits pose?
Notes:
Ask your students to determine which type of danger(s) are posed by high-Q series and parallel resonant circuits, respectively. The answer to this question may seem paradoxical at first: that series resonant circuits whose overall impedance is nearly zero can manifest large voltage drops, while parallel resonant circuits whose overall impedance is nearly infinite can manifest large currents.
Question 19:
Shown here are two frequency response plots (known as Bode plots) for a pair of series resonant circuits. Each circuit has the same inductance and capacitance values, but different resistance values. The öutput" is voltage measured across the resistor of each circuit:
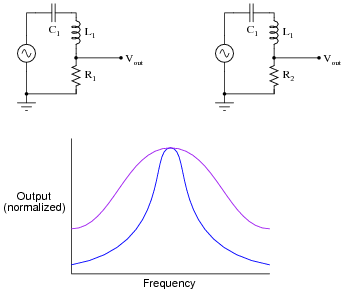
|
|
Which one of these plots represents the response of the circuit with the greatest Q, or quality factor?
Follow-up question: assuming both the inductance and the capacitance values are the same in these two resonant circuits, explain which circuit has the greatest resistance (R1 or R2).
Challenge question: what does the word "normalized" mean with respect to the vertical axis scale of the Bode plot?
Notes:
When your students study resonant filter circuits, they will better understand the importance of Q. For now, though, it is enough that they comprehend the basic notion of how Q impacts the voltage dropped by any one component in a series resonant circuit across a range of frequencies.
Question 20:
The Q, or quality factor, of an inductor circuit is defined by the following equation, where Xs is the series inductive reactance and Rs is the series resistance:
|
We also know that we may convert between series and parallel equivalent AC networks with the following conversion equations:
|
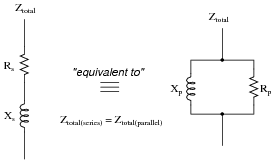
|
|
Series and parallel LR networks, if truly equivalent, should share the same Q factor as well as sharing the same impedance. Develop an equation that solves for the Q factor of a parallel LR circuit.
|
Follow-up question: what condition gives the greatest value for Q, a low parallel resistance or a high parallel resistance? Contrast this against the effects of low versus high resistance in a series LR circuit, and explain both scenarios.
Notes:
This is primarily an exercise in algebraic substitution, but it also challenges students to think deeply about the nature of Q and what it means, especially in the follow-up question.
Question 21:
There is a direct, mathematical relationship between bandwidth, resonant frequency, and Q in a resonant filter circuit, but imagine for a moment that you forgot exactly what that formula was. You think it must be one of these two, but you are not sure which:
|
Based on your conceptual knowledge of how a circuit's quality factor affects its frequency response, determine which of these formulae must be incorrect. In other words, demonstrate which of these must be correct rather than simply looking up the correct formula in a reference book.
Notes:
The purpose of this question is not necessarily to get students to look this formula up in a book, but rather to develop their qualitative reasoning and critical thinking skills. Forgetting the exact form of an equation is not a rare event, and it pays to be able to select between different forms based on a conceptual understanding of what the formula is supposed to predict.
Note that the question asks students to identify the wrong formula, and not to tell which one is right. If all we have are these to formulae to choose from, and a memory too weak to confidently recall the correct form, the best that logic can do is eliminate the wrong formula. The formula making the most sense according to our qualitative analysis may or may not be precisely right, because we could very well be forgetting a multiplicative constant (such as 2 p).
Question 22:
Suppose you have a 110 mH inductor, and wish to combine it with a capacitor to form a band-stop filter with a "notch" frequency of 1 kHz. Draw a schematic diagram showing what the circuit would look like (complete with input and output terminals) and calculate the necessary capacitor size to do this, showing the equation you used to solve for this value. Also, calculate the bandwidth of this notch filter, assuming the inductor has an internal resistance of 20 ohms, and that there is negligible resistance in the rest of the circuit.
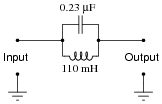
|
|
The bandwidth of this 1 kHz notch filter is approximately 29 Hz.
Follow-up question: suppose you looked around but could not find a capacitor with a value of 0.23 mF. What could you do to obtain this exact capacitance value? Be as specific and as practical as you can in your answer!
Notes:
In my answer I used the series-resonant formula fr = [1/(2 p�{LC})], since the series formula gives good approximations for parallel resonant circuits with Q factors in excess of 10.
The follow-up question is very practical, since it is often common to need a component value that is non-standard. Lest any of your students suggest obtaining a variable capacitor for this task, remind them that variable capacitors are typically rated in the pico-Farad range, and would be much too small for this application.
Question 23:
Shown here are two frequency response plots (known as Bode plots) for a pair of series resonant circuits with the same resonant frequency. The öutput" is voltage measured across the resistor of each circuit:
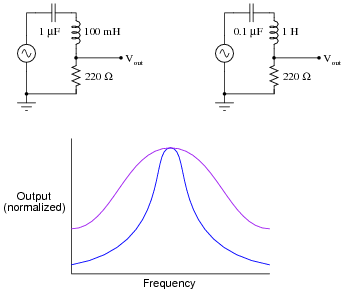
|
|
Determine which plot is associated with which circuit, and explain your answer.
Follow-up question: what kind of instrument(s) would you use to plot the response of a real resonant circuit in a lab environment? Would an oscilloscope be helpful with this task? Why or why not?
Notes:
Discuss with your students why the LC circuit with the greatest L/C ratio has the steeper response, in terms of reactances of the respective components at the resonant frequency.
The purpose of this question is to get students to realize that not all resonant circuits with identical resonant frequencies are alike! Even with ideal components (no parasitic effects), the frequency response of a simple LC circuit varies with the particular choice of component values. This is not obvious from inspection of the resonant frequency formula:
|
Question 24:
Given the unavoidable presence of parasitic inductance and/or capacitance in any electronic component, what does this mean in terms of resonance for single components in AC circuits?
Follow-up question: at what frequency would you expect a component to self-resonate? Would this be a very low frequency, a very high frequency, or a frequency within the circuit's normal operating range? Explain your answer.
Notes:
This question grew out of several years' worth of observations, where students would discover self-resonant effects in large ( > 1 Henry) inductors at modest frequencies. Being a recurring theme, I thought it prudent to include this question within my basic electronics curriculum.
One component that tends to be more immune to self-resonance than others is the lowly resistor, especially resistors of large value. Ask your students why they think this might be. A mechanical analogy to self-resonance is the natural frequency of vibration for an object, given the unavoidable presence of both elasticity and mass in any object. The mechanical systems most immune to vibratory resonance, though, are those with a high degree of intrinsic friction.
Question 25:
A capacitor has been connected in parallel with the solenoid coil to minimize arcing of the switch contacts when opened:
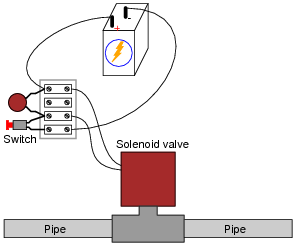
|
|
The only problem with this solution is, resonance between the capacitor and the solenoid coil's inductance is causing an oscillating voltage (commonly known as ringing) to appear across the terminals of each. This high-frequency "ringing" is generating bursts of radio interference whenever the switch contacts open. Radio interference is not good.
You know that the underlying cause of this "ringing" is resonance, yet you cannot simply remove the capacitor from the circuit because you know that will result in decreased operating life for the switch contacts, as the solenoid's inductive "kickback" will cause excessive arcing. How do you overcome this problem without creating another problem?
Follow-up question: besides shortening the life of the switch, what other undesirable effects can switch ärcing" have? Can you think of any scenarios where an arcing switch could pose a safety hazard?
Notes:
Besides posing a practical problem-solving scenario to students, this question is a good lead-in to the topic of antiresonance. Be sure to allow plenty of class discussion time for this question, as many topics are likely to be covered as students discuss alternative problem-solving strategies.
Question 26:
An alternative to "tank circuit" combinations of L and C in many electronic circuits is a small device known as a crystal. Explain how a "crystal" may take the place of a tank circuit, and how it functions.
Notes:
My answer here is purposefully vague, to inspire students to research on their own.
