Peak, average, and RMS measurements
Question 1:
How is it possible to assign a fixed value of voltage or current (such as "120 volts") to an AC electrical quantity that is constantly changing, crossing 0 volts, and reversing polarity?
Notes:
Before you discuss "RMS" values with your students, it is important to cover the basic idea of how to assign fixed values to quantities that change over time. Since AC waveforms are cyclic (repeating), this is not as difficult to do as one might think.
Question 2:
Suppose a DC power source with a voltage of 50 volts is connected to a 10 W load. How much power will this load dissipate?
Now suppose the same 10 W load is connected to a sinusoidal AC power source with a peak voltage of 50 volts. Will the load dissipate the same amount of power, more power, or less power? Explain your answer.
Notes:
There are many analogies to explain this discrepancy between the two "50 volt" sources. One is to compare the physical effort of a person pushing with a constant force of 50 pounds, versus someone who pushes intermittently with only a peak force of 50 pounds.
Question 3:
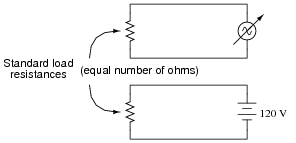
Suppose that a variable-voltage AC source is adjusted until it dissipates the exact same amount of power in a standard load resistance as a DC voltage source with an output of 120 volts:
|
|
In this condition of equal power dissipation, how much voltage is the AC power supply outputting? Be as specific as you can in your answer.
Notes:
Ask your students, "how much peak voltage is the AC power source outputting? More or less than 120 volts?"
If one of your students claims to have calculated the peak voltage as 169.7 volts, ask them how they arrived at that answer. Then ask if that answer depends on the shape of the waveform (it does!). Note that the question did not specify a ßinusoidal" wave shape. Realistically, an adjustable-voltage AC power supply of substantial power output will likely be sinusoidal, being powered from utility AC power, but it could be a different wave-shape, depending on the nature of the source!
Question 4:
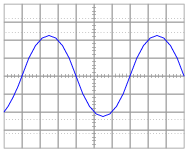
Determine the RMS amplitude of this sinusoidal waveform, as displayed by an oscilloscope with a vertical sensitivity of 0.2 volts per division:
|
|
Notes:
Students must properly interpret the oscilloscope's display, then correctly convert to RMS units, in order to obtain the correct answer for this question.
Question 5:
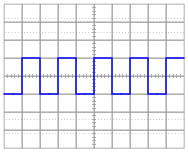
Determine the RMS amplitude of this square-wave signal, as displayed by an oscilloscope with a vertical sensitivity of 0.5 volts per division:
|
|
Notes:
Many electronics students I've talked to seem to think that the RMS value of a waveform is always [(�2)/2], no matter what the waveshape. Not true, as evidenced by the answer for this question!
Students must properly interpret the oscilloscope's display in order to obtain the correct answer for this question. The "conversion" to RMS units is really non-existent, but I want students to be able to explain why it is and not just memorize this fact.
Question 6:
Suppose two voltmeters are connected to source of "mains" AC power in a residence, one meter is analog (D'Arsonval PMMC meter movement) while the other is true-RMS digital. They both register 117 volts while connected to this AC source.
Suddenly, a large electrical load is turned on somewhere in the system. This load both reduces the mains voltage and slightly distorts the shape of the waveform. The overall effect of this is average AC voltage has decreased by 4.5% from where it was, while RMS AC voltage has decreased by 6% from where it was. How much voltage does each voltmeter register now?
True-RMS digital voltmeter now registers: 110 volts
Notes:
Students sometimes have difficulty grasping the significance of PMMC meter movements being äverage-responding" rather than RMS-responding. Hopefully, the answer to this question will help illuminate this subject more.
Question 7:
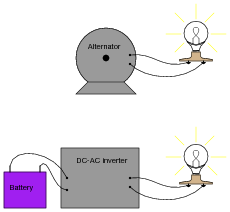
An electromechanical alternator (AC generator) and a DC-DC inverter both output the same RMS voltage, and deliver the same amount of electrical power to two identical loads:
|
|
However, when measured by an analog voltmeter, the inverter's output voltage is slightly greater than the alternator's output voltage. Explain this discrepancy in measurements.
Notes:
Remember, most analog meter movement designs respond to the average value of a waveform, not its RMS value. If the proportionality between a waveform's average and RMS values ever change, the relative indications of a true-RMS instrument and an average-based (calibrated to read RMS) instrument will change as well.
Question 8:
Is the deflection of an analog AC meter movement proportional to the peak, average, or RMS value of the waveform measured? Explain your answer.
Follow-up question: does this mean an average-responding meter movement cannot be calibrated to indicate in RMS units?
Challenge question: why do hot-wire and electrodynamometer meter movements provide true RMS indications, while most other movement designs indicate based on the signal's average value?
Notes:
Students often confuse the terms äverage" and "RMS", thinking they are interchangeable. Discuss the difference between these two terms, both mathematically and practically. While the concepts may seem similar at first, the details are actually quite different.
The question of whether an average-responding instrument can be calibrated to register in RMS units is very practical, since the vast majority of multimeters are calibrated this way. Because the proportionality between the average and RMS values of an AC waveform are dependent on the shape of the waveform, a certain wave-shape must be assumed in order to accurately calibrate an average-responding meter movement for RMS measurement. The assumed wave-shape, of course, is sinusoidal.
Question 9:
In calculating the size of wire necessary to carry alternating current to a high-power load, which type of measurement is the best to use for current: peak, average, or RMS? Explain why.
Notes:
A clue to answering this question is this: what actually happens when the ampacity rating of a conductor is exceeded? Why, exactly, is overcurrent a bad thing for conductors in general?
It is important for students to recognize the value of RMS measurements: why do we use them, and in what applications are they the most appropriate type of measurement to use in certain calculations? Ask your students what other applications might best use RMS voltage and current measurements as opposed to peak or average.
Question 10:
In calculating the thickness of insulators for high-voltage AC power lines, which type of measurement is the best to use for voltage: peak, average, or RMS? Explain why.
Notes:
A closely related subject is insulator breakdown, or dielectric strength. What actually happens when the dielectric strength rating of an insulator is exceeded?
