Switched capacitor circuitry
Question 1:
Write an equation describing the precise mathematical relationship between electric charge (Q), capacitance (C), and voltage (V).
Follow-up question: calculate the amount of charge stored in a 330 mF capacitor charged with a voltage of 12 volts.
Notes:
This is one of those equations usually discussed somewhere in the first few months of basic electronics education, and promptly forgotten by most. It can be very useful, however, when dealing with charge pumps and other switched-capacitor circuitry.
Question 2:
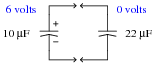
What would happen if a 10 mF capacitor, charged to a voltage of 6 volts, were connected to a completely discharged (0 volts) 22 mF capacitor?
|
|
What would the voltage(s) be across each capacitor, after enough time had passed for complete equalization to occur?
Notes:
The most important aspect of your students' answers is how they arrived at them. There is more than one way to solve this problem!
Question 3:
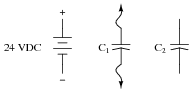
What would happen to the voltage across capacitor C2 if the following steps were followed, over and over again:
|
|
- �
- Connect capacitor C1 to battery, allow to fully charge
- �
- Disconnect capacitor C1 from battery
- �
- Connect capacitor C1 to capacitor C2, allow for charges to equalize
- �
- Disconnect capacitor C1 from capacitor C2
- �
- Repeat
Challenge question: how do the relative sizes of the capacitors (in Farads) affect this process? For example, what if C1 = 10 mF and C2 = 470 mF? Or, what if C1 = 330 mF and C2 = 2.2 mF? Explain your answer.
Notes:
This question previews flying capacitor circuits.
Question 4:
Describe what happens to Vout (the voltage across capacitor C4) as time goes on, assuming the relay is continuously toggled by the oscillator circuit at a high frequency. Assume that the input voltage (Vin) is constant over time:

|
|
This type of circuit is often referred to as a flying capacitor circuit, with C3 being the "flying" capacitor. Explain why this is, and what possible benefit might be realized by using a flying capacitor circuit to sample a voltage.
Notes:
I once worked for a company where thousands of these "flying capacitor" circuits were used to sample voltage across numerous series-connected electrochemical reduction cells, whose common-mode voltage could easily exceed 500 volts DC! This primitive technology provided isolation so that the data acquisition circuitry did not have to deal with that high common-mode voltage.
Incidentally, the relays we used were hermetically sealed, mercury-wetted contact, reed relays. These relays had a surprisingly long life, often several years! They were cycled at around 20 Hz, for several cycles, about once every minute (24 hours per day, 365 days per year).
Question 5:
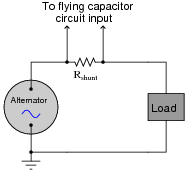
Suppose an engineer decided to use a flying capacitor circuit to sample voltage across a shunt resistor, to measure AC current from an electrical generator:
|
|
The frequency of the alternator's output is 50 Hz. How does this affect the design of the flying capacitor circuit, so we ensure a fairly accurate reproduction of the AC signal at the output of the flying capacitor circuit? Generalize your answer to cover all conditions where the input signal varies over time.
Challenge question: if you were the technician or engineer on this project, what switching frequency would you suggest for the flying capacitor circuit? How would this criterion affect the design of the flying capacitor circuit itself (capacitor values, relay versus transistor switches)?
Notes:
Ask your students to sketch an approximation of the flying capacitor circuit's output waveform for different sampling frequencies. This question is a great lead-in to a discussion on Nyquist frequency, if your students are ready for it!
An important aspect of this question is for students to generalize from this specific circuit example to all systems where signals are sampled along discrete time intervals. In modern electronic circuitry, especially data acquisition circuitry, sample time can be a significant issue. In my experience, it is one of the primary reasons for digital systems giving poor results.
Question 6:
In this circuit, a capacitor is alternately connected to a voltage source, then a load, by means of two MOSFET transistors that are never conducting at the same time:

|
|
Note: the f1 and f2 pulse signals are collectively referred to as a non-overlapping, two-phase clock.
Consider the average amount of current through the load resistor, as a function of clock frequency. Assume that the ön" resistance of each MOSFET is negligible, so that the time required for the capacitor to charge is also negligible. As the clock frequency is increased, does the load resistor receive more or less average current over a span of several clock cycles? Here is another way to think about it: as the clock frequency increases, does the load resistor dissipate more or less power?
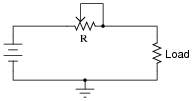
Now suppose we have a simple two-resistor circuit, where a potentiometer (connected as a variable resistor) throttles electrical current to a load:
|
|
It should be obvious in this circuit that the load current decreases as variable resistance R increases. What might not be so obvious is that the aforementioned switched capacitor circuit emulates the variable resistor R in the second circuit, so that there is a mathematical equivalence between f and C in the first circuit, and R in the second circuit, so far as average current is concerned. To put this in simpler terms, the switched capacitor network behaves sort of like a variable resistor.
Calculus is required to prove this mathematical equivalence, but only a qualitative understanding of the two circuits is necessary to choose the correct equivalency from the following equations. Which one properly describes the equivalence of the switched capacitor network in the first circuit to the variable resistor in the second circuit?
|
Be sure to explain the reasoning behind your choice of equations.
Notes:
Perhaps the most important aspect of this question is students' analytical reasoning: how did they analyze the two circuits to arrive at their answers? Be sure to devote adequate class time to a discussion of this, helping the weaker students grasp the concept of switched-capacitor/resistor equivalency by allowing stronger students to present their arguments.
Question 7:
In this circuit, a capacitor is alternately connected in series between a voltage source and a load, then shorted, by means of two MOSFET transistors that are never conducting at the same time:

|
|
Note: the f1 and f2 pulse signals are collectively referred to as a non-overlapping, two-phase clock.
Consider the average amount of current through the load resistor, as a function of clock frequency. Assume that the ön" resistance of each MOSFET is negligible, so that the time required for the capacitor to charge is also negligible. As the clock frequency is increased, does the load resistor receive more or less average current over a span of several clock cycles? Here is another way to think about it: as the clock frequency increases, does the load resistor dissipate more or less power?
Now suppose we have a simple two-resistor circuit, where a potentiometer (connected as a variable resistor) throttles electrical current to a load:
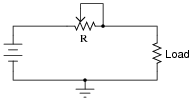
|
|
It should be obvious in this circuit that the load current decreases as variable resistance R increases. What might not be so obvious is that the aforementioned switched capacitor circuit emulates the variable resistor R in the second circuit, so that there is a mathematical equivalence between f and C in the first circuit, and R in the second circuit, so far as average current is concerned. To put this in simpler terms, the switched capacitor network behaves sort of like a variable resistor.
Calculus is required to prove this mathematical equivalence, but only a qualitative understanding of the two circuits is necessary to choose the correct equivalency from the following equations. Which one properly describes the equivalence of the switched capacitor network in the first circuit to the variable resistor in the second circuit?
|
Be sure to explain the reasoning behind your choice of equations.
Notes:
Perhaps the most important aspect of this question is students' analytical reasoning: how did they analyze the two circuits to arrive at their answers? Be sure to devote adequate class time to a discussion of this, helping the weaker students grasp the concept of switched-capacitor/resistor equivalency by allowing stronger students to present their arguments.
Question 8:
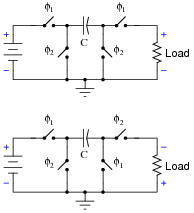
Identify the polarity of voltage across the load resistor in the following switched capacitor circuit (called a transresistor circuit). Note: f1 and f2 are two-phase, non-overlapping clock signals, and the switches are just generic representations of transistors.
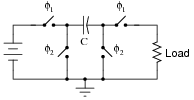
|
|
Identify the polarity of voltage across the load resistor in the following switched capacitor circuit. Note: the only difference between this circuit and the last is the switching sequence.
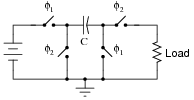
|
|
What difference would it make to the output signal of this operational amplifier circuit if the switching sequence of the switched capacitor network were changed? What difference would it make if the switching frequency were changed?
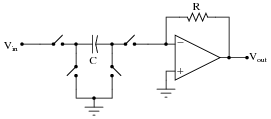
|
|
|
|
The op-amp circuit will act as an inverting or non-inverting amplifier, depending on the switching sequence. Gain will be affected by switching frequency.
Challenge question: the second switched capacitor network is often referred to as a negative resistor equivalent. Explain why.
Notes:
Some of the versatility of switched capacitor networks can be seen in these two circuit examples. Really, they're the same circuit, just operated differently. Discuss with your students how this versatility may be an advantage in circuit design.
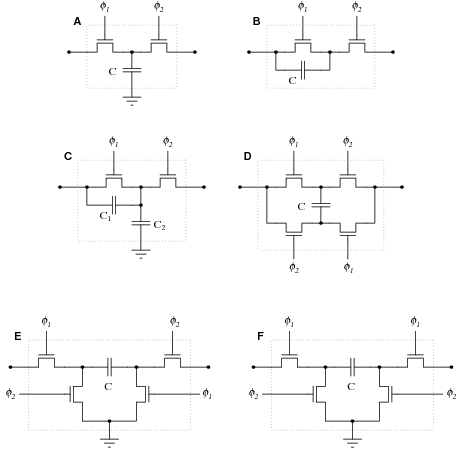
Question 9:
Research the resistance equivalence equations for each of these switched-capacitor networks (using N-channel MOSFETs as switches), describing the emulated resistance (R) as a function of switching frequency (f) and capacitance (C):
|
|
Note: f1 and f2 are two-phase, non-overlapping clock signals.
Circuit B: Series circuit R = [1/fC]
Circuit C: Series-parallel circuit R = [1/(f(C1 + C2))]
Circuit D: Bilinear circuit R = [1/4fC]
Circuit E: Negative transresistor circuit R = - [1/fC] (the negative sign indicates polarity inversion)
Circuit F: Positive transresistor circuit R = [1/fC]
Notes:
The mathematics required to derive these equations directly may be beyond your students' ability, but they should still be able to research them! Some of the networks are directly equivalent to one another, making it easier for your students to associate equations: for instance, circuit F is equivalent to circuit B, and circuit E is the same thing as F except for the polarity inversion. It should not take a great deal of analysis to realize that circuits A and B must have the same equation as well.
Question 10:
Given the fact that a switched-capacitor network has the ability to emulate a variable resistance, what advantage(s) can you think of for using switched-capacitor networks inside of analog integrated circuits? Identify some practical applications of this technology.
I'll let you research (or dream up) some practical applications for this technology.
Notes:
This question could very well lead to an interesting and lively discussion with your students. Once students recognize the equivalence between switched-capacitor networks and resistors, it is a short cognitive leap from there to practical applications where variable resistances would be useful (especially in an integrated circuit environment, where moving parts have traditionally been out of the question).
Question 11:
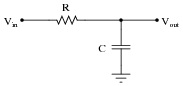
Identify what type of passive filter circuit this is, and then sketch a schematic diagram for an equivalent circuit using a switched-capacitor network instead of a resistor:
|
|
Also, write an equation describing the cutoff frequency in terms of switching frequency and capacitor values.

|
|
|
Note: in order for this circuit to be practical, fswitch >> fsignal.
Notes:
This question asks students to substitute a switched capacitor network for the fixed resistor in the original filter circuit. Similarly, algebraic substitution is required to derive the equation for cutoff frequency.
Question 12:
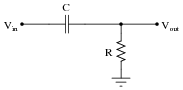
Identify what type of passive filter circuit this is, and then sketch a schematic diagram for an equivalent circuit using a switched-capacitor network instead of a resistor:
|
|
Also, write an equation describing the cutoff frequency in terms of switching frequency and capacitor values.

|
|
|
Note: in order for this circuit to be practical, fswitch >> fsignal.
Notes:
This question asks students to substitute a switched capacitor network for the fixed resistor in the original filter circuit. Similarly, algebraic substitution is required to derive the equation for cutoff frequency.
Question 13:
A 4.7 mF capacitor (Ci) is charged to a voltage of 4 volts, then connected to the inverting input of an operational amplifier (with a 10 mF feedback capacitor, Cf). What happens to the voltages across Ci and Cf? Explain your answer in detail.
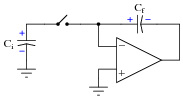
|
|
Notes:
The reason why VCi goes to zero, of course, is a function of the opamp's negative feedback. This aspect of the question provides an excellent opportunity for review of basic opamp principles.
Question 14:
Many switched capacitor circuits require non-overlapping, two-phase clock signals. Shown here is a schematic diagram of a gate circuit that converts a single clock signal into two complementary, non-overlapping clock signals:
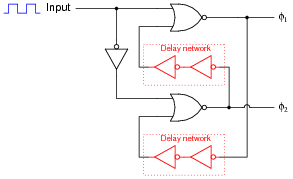
|
|
Assume that the only gates possessing propagation delays are the double-NOT gates (inside the dotted boxes), whose sole purpose it is to provide a short time delay in the feedback signals. Draw a timing diagram showing the two-phase clock signals (f1 and f2) in relation to the input clock waveform, and be prepared to explain how and why this circuit works:
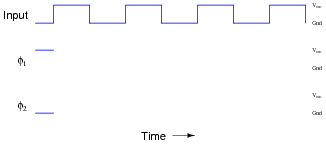
|
|

|
|
Notes:
Although it will be obvious to many of your students, you might want to ask "why do we call the two clock signals non-overlapping?" What, exactly, would an overlapping set of clock signals look like, in comparison?
Question 15:
The fact that switched capacitor networks can behave equivalently to resistors is exploited in a variety of integrated circuits. At first, this may seem strange, as switched capacitor networks generally require at least two switching transistors and a two-phase, non-overlapping clock (in addition to the capacitor itself) in order to function, which seems like a lot of peripheral circuitry compared to a single resistor. What possible advantage is there to using switched capacitor networks in integrated circuits instead of resistors? Support your answer with research, if possible.
There are other advantages to switched capacitor networks, but these are just some of the basic reasons behind their prevalence in modern integrated circuits.
Notes:
Ask your students to explain why switched capacitor networks are less prone to drift than resistors constructed on a semiconductor substrate. Just focus on one source of drift, such as temperature, to simplify the topic. What effect does temperature have on a semiconducting resistor, and why? What effect does temperature have on a capacitor built of semiconductor layers separated by an insulating layer, and why? With discrete components, are capacitors more stable over time than resistors? Why or why not?
