AC waveforms
Question 1:
Radio waves are comprised of oscillating electric and magnetic fields, which radiate away from sources of high-frequency AC at (nearly) the speed of light. An important measure of a radio wave is its wavelength, defined as the distance the wave travels in one complete cycle.
Suppose a radio transmitter operates at a fixed frequency of 950 kHz. Calculate the approximate wavelength (l) of the radio waves emanating from the transmitter tower, in the metric distance unit of meters. Also, write the equation you used to solve for l.
I'll let you find the equation on your own!
Notes:
I purposely omit the velocity of light, as well as the time/distance/velocity equation, so that students will have to do some simple research this calculate this value. Neither of these concepts is beyond high-school level science students, and should pose no difficulty at all for college-level students to find on their own.
Question 2:
What is the difference between DC and AC electricity? Identify some common sources of each type of electricity.
Electrochemical batteries generate DC, as do solar cells. Microphones generate AC when sensing sound waves (vibrations of air molecules). There are many, many other sources of DC and AC electricity than what I have mentioned here!
Notes:
Discuss a bit of the history of AC versus DC in early power systems. In the early days of electric power in the United States of America, there was a heated debate between the use of DC versus AC. Thomas Edison championed DC, while George Westinghouse and Nikola Tesla advocated AC.
It might be worthwhile to mention that almost all the electric power in the world is generated and distributed as AC (Alternating Current), and not as DC (in other words, Thomas Edison lost the AC/DC battle!). Depending on the level of the class you are teaching, this may or may not be a good time to explain why most power systems use AC. Either way, your students will probably ask why, so you should be prepared to address this question in some way (or have them report any findings of their own!).
Question 3:
Alternating current produced by electromechanical generators (or alternators as they are sometimes designated) typically follows a sine-wave pattern over time. Plot a sine wave on the following graph, by tracing the height of a rotating vector inside the circle to the left of the graph:
|
|
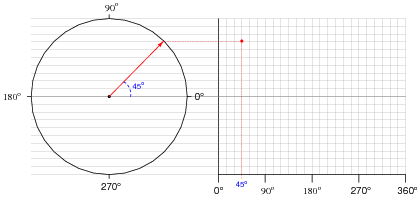
To illustrate the principle here, I will show how the point is plotted for a rotation of 45o:
|
|
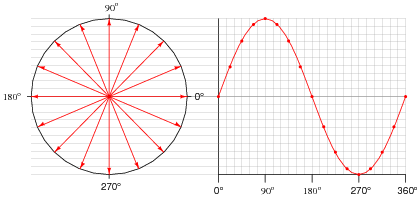
You may wish to use a protractor to precisely mark the angles along the rotation of the circle, in making your sine-wave plot.
|
|
Notes:
For many students, this might be the first time they realize trigonometry functions have anything to do with electricity! That voltage and current in an AC circuit might alternate according to a mathematical function available in their calculators is something of a revelation. Be prepared to discuss why rotating electromagnetic machines naturally produce such waveforms. Also, encourage students to make the cognitive connection between the independent variable of a sine function (angle, expressed in units of degrees in this question) to actual shaft rotation in a real generator.
Question 4:
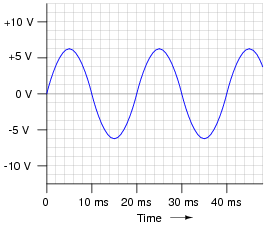
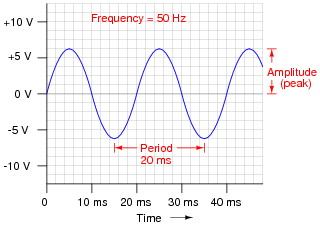
Apply the following terms to this graph of an AC voltage measured over time:
- �
- Frequency
- �
- Period
- �
- Hertz
- �
- Amplitude
|
|
|
|
Notes:
As always, it is more important to be able to apply a term to a real-life example than it is to memorize a definition for that term. In my experience, many students prefer to memorize definitions for terms rather than to go through the trouble of understanding how those terms apply to real life. Make sure students realize just how and why these AC terms apply to a waveform such as this.
Question 5:
Frequency used to be expressed in units of cycles per second, abbreviated as CPS. Now, the standardized unit is Hertz. Explain the meaning of the obsolete frequency unit: what, exactly, does it mean for an AC voltage or current to have x number of "cycles per second?"
Notes:
Encourage your students to discuss the origins of the new unit (Hertz), and how it actually communicates less information about the thing being measured than the old unit (CPS).
Question 6:
If an AC voltage has a frequency of 350 Hz, how long (in time) is its period?
Notes:
It is important for students to realize the reciprocal relationship between frequency and period. One is cycles per second while the other is seconds per cycle.
Question 7:
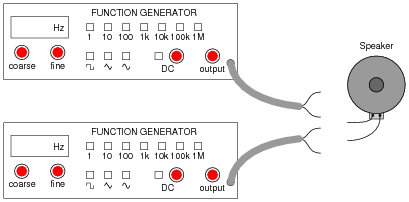
If the only instrument you had in your possession to detect AC voltage signals was an audio speaker, how could you use it to determine which of two AC voltage waveforms has the greatest period?
|
|
Notes:
An audio speaker is an outstanding instrument to use in teaching AC theory, because it makes use of a human sense that most instruments do not. I have constructed a simple headphone-based listening instrument for my own lab use, and have found it invaluable, especially in the absence of an oscilloscope. There is so much the trained ear may discern about an AC waveform based on volume and tone!
Question 8:
Determine the frequency of a waveform having a period of 1.4 milliseconds (1.4 ms).
Notes:
It is important for students to realize the reciprocal relationship between frequency and period. One is cycles per second while the other is seconds per cycle.
Question 9:
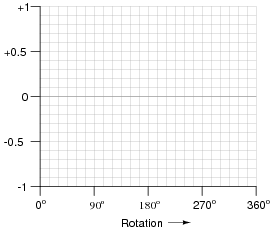
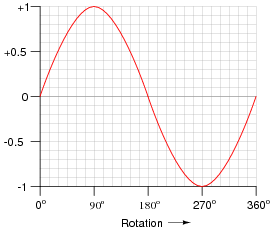
Alternating current produced by electromechanical generators (or alternators as they are sometimes designated) typically follows a sine-wave pattern over time. Using a calculator, or a set of "trig tables," plot a sine wave on the following graph:
|
|
|
|
Notes:
For many students, this might be the first time they realize trigonometry functions have anything to do with electricity! That voltage and current in an AC circuit might alternate according to a mathematical function available in their calculators is something of a revelation. Be prepared to discuss why rotating electromagnetic machines naturally produce such waveforms. Also, encourage students to make the cognitive connection between the independent variable of a sine function (angle, expressed in units of degrees in this question) to actual shaft rotation in a real generator.
Question 10:
Define the following terms:
- �
- Frequency
- �
- Wavelength
- �
- Cycle
- �
- Hertz
- �
- Amplitude
Notes:
The unit "Hertz" is an example of how an implicitly defined label like "cycles per second" (CPS) came to be replaced by one having no objective meaning at all. Similar to how "Celsius" replaced "Centigrade" as the official metric name for a unit of temperature measurement. Pardon me for stepping up on my soapbox here, but changes such as these really irritate me.
It is important to understand that these terms apply to non-electrical phenomena as well as electrical. The wide applicability of such terms allows for easier comprehension. Ask your students to give common examples of these terms in everyday life. Hint: music is an excellent context for this question!
