Multi-stage amplifier
PARTS AND MATERIALS
- Three NPN transistors -- model 2N2222 or 2N3403 recommended (Radio Shack catalog # 276-1617 is a package of fifteen NPN transistors ideal for this and other experiments)
- Two 6-volt batteries
- One 10 kΩ potentiometer, single-turn, linear taper (Radio Shack catalog # 271-1715)
- One 1 MΩ resistor
- Three 100 kΩ resistors
- Three 10 kΩ resistors
CROSS-REFERENCES
Lessons In Electric Circuits, Volume 3, chapter 4: "Bipolar Junction Transistors"
LEARNING OBJECTIVES
- Design of a multi-stage, direct-coupled common-emitter amplifier circuit
- Effect of negative feedback in an amplifier circuit
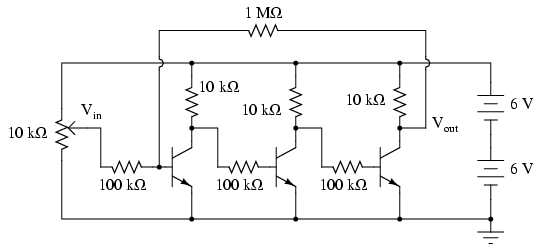
SCHEMATIC DIAGRAM
ILLUSTRATION

INSTRUCTIONS
By connecting three common-emitter amplifier circuit together -- the collector terminal of the previous transistor to the base (resistor) of the next transistor -- the voltage gains of each stage compound to give a very high overall voltage gain. I recommend building this circuit without the 1 MΩ feedback resistor to begin with, to see for yourself just how high the unrestricted voltage gain is. You may find it impossible to adjust the potentiometer for a stable output voltage (that isn't saturated at full supply voltage or zero), the gain being so high.
Even if you can't adjust the input voltage fine enough to stabilize the output voltage in the active range of the last transistor, you should be able to tell that the output-to-input relationship is inverting; that is, the output tends to drive to a high voltage when the input goes low, and vice versa. Since any one of the common-emitter "stages" is inverting in itself, an even number of staged common-emitter amplifiers gives noninverting response, while an odd number of stages gives inverting. You may experience these relationships by measuring the collector-to-ground voltage at each transistor while adjusting the input voltage potentiometer, noting whether or not the output voltage increases or decreases with an increase in input voltage.
Connect the 1 MΩ feedback resistor into the circuit, coupling the collector of the last transistor to the base of the first. Since the overall response of this three-stage amplifier is inverting, the feedback signal provided through the 1 MΩ resistor from the output of the last transistor to the input of the first should be negative in nature. As such, it will act to stabilize the amplifier's response and minimize the voltage gain. You should notice the reduction in gain immediately by the decreased sensitivity of the output signal on input signal changes (changes in potentiometer position). Simply put, the amplifier isn't nearly as "touchy" as it was without the feedback resistor in place.
As with the simple common-emitter amplifier discussed in an earlier experiment, it is a good idea here to make a table of input versus output voltage figures with which you may calculate voltage gain.
Experiment with different values of feedback resistance. What effect do you think a decrease in feedback resistance have on voltage gain? What about an increase in feedback resistance? Try it and find out!
An advantage of using negative feedback to "tame" a high-gain amplifier circuit is that the resulting voltage gain becomes more dependent upon the resistor values and less dependent upon the characteristics of the constituent transistors. This is good, because it is far easier to manufacture consistent resistors than consistent transistors. Thus, it is easier to design an amplifier with predictable gain by building a staged network of transistors with an arbitrarily high voltage gain, then mitigate that gain precisely through negative feedback. It is this same principle that is used to make operational amplifier circuits behave so predictably.
This amplifier circuit is a bit simplified from what you will normally encounter in practical multi-stage circuits. Rarely is a pure common-emitter configuration (i.e. with no emitter-to-ground resistor) used, and if the amplifier's service is for AC signals, the inter-stage coupling is often capacitive with voltage divider networks connected to each transistor base for proper biasing of each stage. Radio-frequency amplifier circuits are often transformer-coupled, with capacitors connected in parallel with the transformer windings for resonant tuning.
COMPUTER SIMULATION
Schematic with SPICE node numbers:
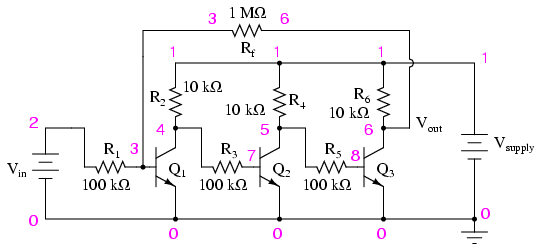
Netlist (make a text file containing the following text, verbatim):
Multi-stage amplifier vsupply 1 0 dc 12 vin 2 0 r1 2 3 100k r2 1 4 10k q1 4 3 0 mod1 r3 4 7 100k r4 1 5 10k q2 5 7 0 mod1 r5 5 8 100k r6 1 6 10k q3 6 8 0 mod1 rf 3 6 1meg .model mod1 npn bf=200 .dc vin 0 2.5 0.1 .plot dc v(6,0) v(2,0) .end
This simulation plots output voltage against input voltage, and allows comparison between those variables in numerical form: a list of voltage figures printed to the left of the plot. You may calculate voltage gain by taking any two analysis points and dividing the difference in output voltages by the difference in input voltages, just like you do for the real circuit.
Experiment with different feedback resistance values (rf) and see the impact on overall voltage gain. Do you notice a pattern? Here's a hint: the overall voltage gain may be closely approximated by using the resistance figures of r1 and rf, without reference to any other circuit component!
