Algebraic substitution for electric circuits
Question 1:
There are two basic Ohm's Law equations: one relating voltage, current, and resistance; and the other relating voltage, current, and power (the latter equation is sometimes known as
Joule's Law rather than Ohm's Law):
In electronics textbooks and reference books, you will find twelve different variations of these two equations, one solving for each variable in terms of a unique pair of two other variables. However, you need not memorize all twelve equations if you have the ability to algebraically manipulate the two simple equations shown above.
Demonstrate how algebra is used to derive the ten öther" forms of the two Ohm's Law / Joule's Law equations shown here.
Reveal Answer
I won't show you how to do the algebraic manipulations, but I will show you the ten other equations. First, those equations that may be derived strictly from E = I R:
Next, those equations that may be derived strictly from P = I E:
Next, those equations that may be derived by using algebraic
substitution between the original two equations given in the question:
And finally, those equations which may be derived from manipulating the last two power equations:
Notes:
Algebra is an extremely important tool in many technical fields. One nice thing about the study of electronics is that it provides a relatively simple context in which fundamental algebraic principles may be learned (or at least illuminated).
The same may be said for calculus concepts as well: basic principles of derivative and integral (with respect to time) may be easily applied to capacitor and inductor circuits, providing students with an accessible context in which these otherwise abstract concepts may be grasped. But calculus is a topic for later worksheet questions . . .
Hide Answer
Question 2:
The Q factor of a series inductive circuit is given by the following equation:
Likewise, we know that inductive reactance may be found by the following equation:
We also know that the resonant frequency of a series LC circuit is given by this equation:
Through algebraic substitution, write an equation that gives the Q factor of a series resonant LC circuit exclusively in terms of L, C, and R, without reference to reactance (X) or frequency (f).
Reveal Answer
Notes:
This is merely an exercise in algebra. However, knowing how these three component values affects the Q factor of a resonant circuit is a valuable and practical insight!
Hide Answer
Question 3:
We know that the current in a series circuit may be calculated with this formula:
We also know that the voltage dropped across any single resistor in a series circuit may be calculated with this formula:
Combine these two formulae into one, in such a way that the I variable is eliminated, leaving only E
R expressed in terms of E
total, R
total, and R.
Reveal Answer
|
ER = Etotal |
�
�
|
|
R
Rtotal
|
|
�
�
|
|
|
Follow-up question: algebraically manipulate this equation to solve for E
total in terms of all the other variables. In other words, show how you could calculate for the amount of total voltage necessary to produce a specified voltage drop (E
R) across a specified resistor (R), given the total circuit resistance (R
total).
Notes:
Though this "voltage divider formula" may be found in any number of electronics reference books, your students need to understand how to algebraically manipulate the given formulae to arrive at this one.
Hide Answer
Question 4:
Substitution is a technique whereby we let a variable represent (stand in the place of) another variable or an expression made of other variables. One application where we might use substitution is when we must manipulate an algebraic expression containing a lot of similar-looking variables, as is often the case with science problems.
Take this series-parallel resistor circuit for example:
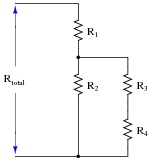
The equation expressing total resistance as a function of the four resistor values looks like this:
|
Rtotal = R1 +
|
R2 (R3 + R4)
R2 + R3 + R4
|
|
|
Now imagine being asked to manipulate this equation to solve for R
3. When the only visual feature distinguishing each of the variables is the subscript (
total,
1,
2,
3, or
4), it becomes very easy to lose track of where one is in the algebraic manipulation. A very common mistake is to exchange or needlessly repeat subscripts during the process, effectively mis-placing one or more variables. To help avoid such mistakes, you may
substitute different letter variables for R
total, R
1, R
2, R
3, and R
4 like this:
-
|
|
Original variable
|
New variable
|
|
|
Rtotal
|
y
|
|
|
R1
|
a
|
|
|
R2
|
b
|
|
|
R3
|
c
|
|
|
R4
|
d
|
|
|
|
y = a +
|
b (c + d)
b + c + d
|
|
|
After doing the algebraic manipulation to solve for c (R
3), the equation looks like this:
|
c =
|
(y-a)(b+d) - bd
a + b - y
|
|
|
Back-substitute the original R variables in place of a, b, c, d, and y as you see them in the above equation to arrive at a form that directly relates to the schematic diagram.
Reveal Answer
|
R3 =
|
(Rtotal-R1)(R2 + R4) - R2 R4
R1 + R2 - Rtotal
|
|
|
Challenge question: show all the steps you would take to solve for R
3 in the original equation.
Notes:
Here I show an application of substitution that is useful only because the human brain has difficulty distinguishing similar-looking symbols. More powerful uses of algebraic substitution exist, of course, but this is a start for students who have never seen the concept before.
Hide Answer
Question 5:
Substitution is a technique whereby we let a variable represent (stand in the place of) another variable or an expression made of other variables. One application where we might use substitution is when we must manipulate an algebraic expression containing multiple instances of the same sub-expression. For example, suppose we needed to manipulate this equation to solve for c:
|
1 =
|
a + b(d2 - f2) + c
d2 - f2
|
|
|
The sub-expression d
2 - f
2 appears twice in this equation. Wouldn't it be nice if we had something simpler to put in its place during the time we were busy manipulating the equation, if for no other reason than to have less variables to write on our paper while showing all the steps to our work? Well, we can do this!
Substitute the variable x for the sub-expression d
2 - f
2, and then solve for c. When you are done manipulating the equation, back-substitute d
2 - f
2 in place of x.
Reveal Answer
Original equation:
|
1 =
|
a + b(d2 - f2) + c
d2 - f2
|
|
|
After substituting x:
After manipulating the equation to solve for c:
Back-substituting the original sub-expression in place of x:
Notes:
Here I show an application of substitution that is useful only because the human brain has an easier time dealing with a single symbol than with a collection of different symbols. More powerful uses of algebraic substitution exist, of course, but this is a start for students who are new to the concept.
Hide Answer
Question 6:
Substitution is the term we give to the mathematical equivalence of one variable to one or more other variables in an expression. It is a fundamental principle used to combine two or more equations into a single equation (among other things).
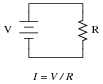
For example, we know that the formula for calculating current in a simple one-resistor circuit is as follows:
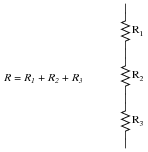
We also know that the total resistance (R) of a three-resistor series circuit is as follows:
Combine these two equations together using substitution so that we have a single equation for calculating current I in a three-resistor series circuit given the source voltage V and each resistance value R
1, R
2, and R
3:
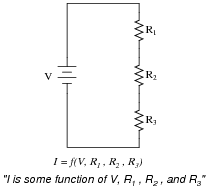
In other words, you need to have as your answer a single equation that begins with "I = " and has all the variables V, R
1, R
2, and R
3 on the other side of the ëqual" sign.
Reveal Answer
Notes:
I like to speak of the process of substitution in terms of definitions for variables. In this particular case, R1 + R2 + R3 is a definition for R that we put in R's place in the first equation (I = V/R).
The notation shown in the third schematic, I = f(V, R1, R2, R3), is known as function notation. It merely means that the value of I is determined by the values of all those variables within the parentheses, rather than just one.
Hide Answer
Question 7:
We know that the voltage in a parallel circuit may be calculated with this formula:
We also know that the current through any single resistor in a parallel circuit may be calculated with this formula:
Combine these two formulae into one, in such a way that the E variable is eliminated, leaving only I
R expressed in terms of I
total, R
total, and R.
Reveal Answer
|
IR = Itotal |
�
�
|
|
Rtotal
R
|
|
�
�
|
|
|
How is this formula similar, and how is it different, from the "voltage divider" formula?
Notes:
Though this "current divider formula" may be found in any number of electronics reference books, your students need to understand how to algebraically manipulate the given formulae to arrive at this one.
At first it may seem as though the two divider formulae (voltage versus current) are easy to confuse. Is it [R/(Rtotal)] or [(Rtotal)/R]? However, there is a very simple way to remember which fraction belongs with which formula, based on the numerical value of that fraction. Mention this to your students and at least one of them will be sure to recognize the pattern.
Hide Answer
Question 8:
Suppose we only knew the emitter and base currents for an operating transistor and wished to calculate
b from that information. We would need a definition of beta cast in terms of I
E and I
B instead of I
C and I
B.
Apply algebraic substitution to the formula
b = [(I
C)/(I
B)] so that beta (
b) is defined in terms of I
E and I
B. You may find the following equation helpful in your work:
Reveal Answer
Notes:
This question is nothing more than an exercise in algebraic manipulation.
Hide Answer
Question 9:
The resistance of a piece of copper wire at temperature T (in degrees Celsius) is given by the following formula:
|
RT = Ro [1 + 0.004041(T - 20)]
|
|
Suppose you wished to alter this formula so it could accept values for T in units of degrees Fahrenheit instead of degrees Celsius. Suppose also that the only formula you are able to find for converting between Fahrenheit (T
F) and Celsius (T
C) is this one:
Combined these two formulae into one solving for the resistance of a copper wire sample (R
T) at a specific temperature in degrees Celsius (T
C), given the specimen's "reference" resistance (R
o) at 20
o Celsius (room temperature).
Reveal Answer
|
RT = Ro |
�
�
|
1 + 0.004041
|
�
�
|
5
9
|
TF - 37.
|
77
|
�
�
|
�
�
|
|
|
Notes:
Solving this algebraic problem requires both manipulation of the temperature equation and substitution of variables. One important detail I incorporated into this question is the lack of a subscript for T in the original resistance formula. In the first sentence I identify that temperature as being in degrees Celsius, but since there is no other T variables in the equation, I did not have to include a "C" subscript. When students look to the Celsius-Fahrenheit conversion formula to substitute into the resistance formula, they must decide which T in the conversion formula to use, TF or TC. Here, I purposely wrote the conversion formula in terms of TF to see how many students would blindly substitute TF for T in the resistance formula instead of properly identifying TC as the variable to substitute and doing the work of manipulation.
Far from being a "trick" question, this scenario is very realistic. Formulae found in reference manuals do not necessarily use standardized variables, but rather cast their variables according to context. Multiple formulae will most likely not be written with identical subscripted variables just waiting to be substituted. It is the domain of the intelligent technician, engineer, or scientist to figure out what variables are appropriate to substitute based on context!
Hide Answer
Question 10:
A bipolar junction transistor parameter similar to
b is älpha," symbolized by the Greek letter
a. It is defined as the ratio between collector current and emitter current:
Apply algebraic substitution to this formula so that alpha is defined as a
function of beta:
a = f(
b). In other words, substitute and manipulate this equation until you have alpha by itself on one side and no variable except beta on the other.
You may find the following equations helpful in your work:
Reveal Answer
Follow-up question: what range of values might you expect for
a, with a typical transistor?
Notes:
This question is nothing more than an exercise in algebraic manipulation.
Hide Answer
Question 11:
The Q, or
quality factor, of an inductor circuit is defined by the following equation, where X
s is the series inductive reactance and R
s is the series resistance:
We also know that we may convert between series and parallel equivalent AC networks with the following conversion equations:
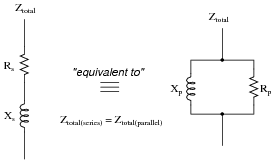
Series and parallel LR networks, if truly equivalent, should share the same Q factor as well as sharing the same impedance. Develop an equation that solves for the Q factor of a
parallel LR circuit.
Reveal Answer
Follow-up question: what condition gives the greatest value for Q, a low parallel resistance or a high parallel resistance? Contrast this against the effects of low versus high resistance in a series LR circuit, and explain both scenarios.
Notes:
This is primarily an exercise in algebraic substitution, but it also challenges students to think deeply about the nature of Q and what it means, especially in the follow-up question.
Hide Answer
Question 12:
The equation relating probability of continued performance for a component or a system versus time may be expressed as follows:
Where,
x = Probability (a number between 0 and 1, inclusive)
e = Euler's constant (
� 2.7182818)
t = Time of continuous operation
m = Mean Time Between Failure of the component or system
The unit of time for both t and m must be the same. That is, if t is measured in years, then m must also be expressed in years or else the equation will give very misleading answers.
Suppose, though, we were given m in years, and the operating time t in
days. Substitute the relationship t
d = 365 t
y into the reliability equation so that we will have a new equation that can take t in days (t
d) and m in years, and still provide the correct answer.
Reveal Answer
Notes:
This is really nothing more than a simple exercise in mathematical substitution.
The equation came from the Standard Handbook of Engineering Calculations by Tyler G Hicks, P.E. (1972), page 5-21.
Hide Answer
Question 13:
The voltage-dependent capacitance of a
varactor diode is given by the following equation:
Where,
C
J = Junction capacitance
C
o = Junction capacitance with no applied voltage
V = Applied reverse junction voltage
Combine this equation with the standard equation for frequency in a resonant LC circuit to arrive at a new equation giving resonant frequency in terms of C
o, V, and L.
Reveal Answer
Notes:
Ask your students what type of circuit this equation might apply in.
Hide Answer





