Miscellaneous diode applications
Question 1:
| Don't just sit there! Build something!! |
Learning to mathematically analyze circuits requires much study and practice. Typically, students practice by working through lots of sample problems and checking their answers against those provided by the textbook or the instructor. While this is good, there is a much better way.
You will learn much more by actually building and analyzing real circuits, letting your test equipment provide the änswers" instead of a book or another person. For successful circuit-building exercises, follow these steps:
- 1.
- Carefully measure and record all component values prior to circuit construction, choosing resistor values high enough to make damage to any active components unlikely.
- 2.
- Draw the schematic diagram for the circuit to be analyzed.
- 3.
- Carefully build this circuit on a breadboard or other convenient medium.
- 4.
- Check the accuracy of the circuit's construction, following each wire to each connection point, and verifying these elements one-by-one on the diagram.
- 5.
- Mathematically analyze the circuit, solving for all voltage and current values.
- 6.
- Carefully measure all voltages and currents, to verify the accuracy of your analysis.
- 7.
- If there are any substantial errors (greater than a few percent), carefully check your circuit's construction against the diagram, then carefully re-calculate the values and re-measure.
When students are first learning about semiconductor devices, and are most likely to damage them by making improper connections in their circuits, I recommend they experiment with large, high-wattage components (1N4001 rectifying diodes, TO-220 or TO-3 case power transistors, etc.), and using dry-cell battery power sources rather than a benchtop power supply. This decreases the likelihood of component damage.
As usual, avoid very high and very low resistor values, to avoid measurement errors caused by meter "loading" (on the high end) and to avoid transistor burnout (on the low end). I recommend resistors between 1 kW and 100 kW.
One way you can save time and reduce the possibility of error is to begin with a very simple circuit and incrementally add components to increase its complexity after each analysis, rather than building a whole new circuit for each practice problem. Another time-saving technique is to re-use the same components in a variety of different circuit configurations. This way, you won't have to measure any component's value more than once.
Notes:
It has been my experience that students require much practice with circuit analysis to become proficient. To this end, instructors usually provide their students with lots of practice problems to work through, and provide answers for students to check their work against. While this approach makes students proficient in circuit theory, it fails to fully educate them.
Students don't just need mathematical practice. They also need real, hands-on practice building circuits and using test equipment. So, I suggest the following alternative approach: students should build their own "practice problems" with real components, and try to mathematically predict the various voltage and current values. This way, the mathematical theory "comes alive," and students gain practical proficiency they wouldn't gain merely by solving equations.
Another reason for following this method of practice is to teach students scientific method: the process of testing a hypothesis (in this case, mathematical predictions) by performing a real experiment. Students will also develop real troubleshooting skills as they occasionally make circuit construction errors.
Spend a few moments of time with your class to review some of the "rules" for building circuits before they begin. Discuss these issues with your students in the same Socratic manner you would normally discuss the worksheet questions, rather than simply telling them what they should and should not do. I never cease to be amazed at how poorly students grasp instructions when presented in a typical lecture (instructor monologue) format!
A note to those instructors who may complain about the "wasted" time required to have students build real circuits instead of just mathematically analyzing theoretical circuits:
What is the purpose of students taking your course?
If your students will be working with real circuits, then they should learn on real circuits whenever possible. If your goal is to educate theoretical physicists, then stick with abstract analysis, by all means! But most of us plan for our students to do something in the real world with the education we give them. The "wasted" time spent building real circuits will pay huge dividends when it comes time for them to apply their knowledge to practical problems.
Furthermore, having students build their own practice problems teaches them how to perform primary research, thus empowering them to continue their electrical/electronics education autonomously.
In most sciences, realistic experiments are much more difficult and expensive to set up than electrical circuits. Nuclear physics, biology, geology, and chemistry professors would just love to be able to have their students apply advanced mathematics to real experiments posing no safety hazard and costing less than a textbook. They can't, but you can. Exploit the convenience inherent to your science, and get those students of yours practicing their math on lots of real circuits!
Question 2:
A technician builds her own audio test set for use in troubleshooting audio electronic circuitry. The test set is essentially a sensitive detector, allowing low-power audio signals to be heard:
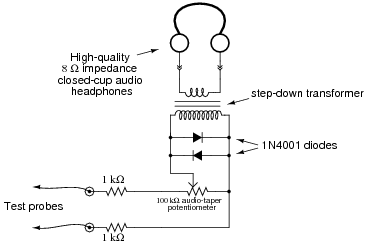
|
|
What purpose do the two diodes serve in this circuit? Hint: if you remove the diodes from the circuit, you will not be able to hear the difference in most cases!
Review question: the purpose of the transformer is to increase the effective impedance of the headphones, from 8 W to a much larger value. Calculate this larger value, given a transformer turns ratio of 22:1.
Notes:
My first encounter with this application of diodes came when I was quite young, soldering together a kit multimeter. I was very confused why the meter movement had two diodes connected to it in parallel like this. All I knew about diodes at the time was that they acted as one-way valves for electricity. I did not understand that they had a substantial forward voltage drop, which is the key to understanding how they work in applications such as this. While this may seem to be a rather unorthodox use of diodes, it is actually rather common.
Incidentally, I highly recommend that students build such an audio test set for their own experimental purposes. Even with no amplifier, this instrument is amazingly sensitive. An inexpensive 120 volt/6 volt step-down power transformer works well as an impedance-matching transformer, and is insulated enough to provide a good margin of safety (electrical isolation) for most applications. An old microwave over power transformer works even better (when used in a step-down configuration), giving several thousand volts worth of isolation between primary and secondary windings.
The circuit even works to detect DC signals and AC signals with frequencies beyond the audio range. By making and breaking contact with the test probe(s), ßcratching" sounds will be produced if a signal of sufficient magnitude is present. With my cheap "Radio Shack" closed-cup headphones, I am able to reliably detect DC currents of less than 0.1 mA with my detector! Your mileage may vary, depending on how good your hearing is, and how sensitive your headphones are.
I have used my own audio detector many times in lieu of an oscilloscope to detect distortion in audio circuits (very rough assessments, mind you, not precision at all) and even as a detector of DC voltage (detecting the photovoltaic output voltage of a regular LED). It may be used as a sensitive "null" instrument in both AC and DC bridge circuits (again, DC detection requires you to make and break contact with the circuit, listening for "clicking" or ßcratching" sounds in the headphones).
Another fun thing to do with this detector is connect it to an open coil of wire and "listen" for AC magnetic fields. Place such a coil near a working computer hard drive, and you can hear the read/write head servos in action!
If it isn't clear to you already, I am very enthusiastic about the potential of this circuit for student engagement and learning . . .
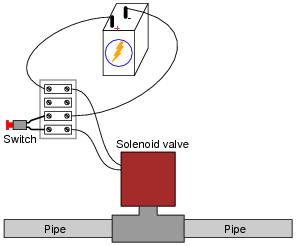
Question 3:
When the pushbutton switch is actuated in this circuit, the solenoid valve energizes:
|
|
The only problem with this simple circuit is that the switch contacts suffer from extensive arcing caused each time the solenoid is de-energized. One way to combat this arcing, though, is to connect an ordinary rectifying diode in parallel with the solenoid like this:
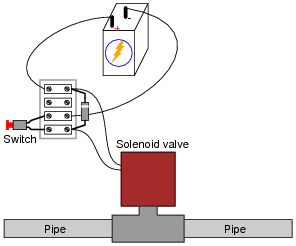
|
|
Explain what causes the excessive arcing at the switch contacts, and how the presence of a diode in the circuit completely eliminates it.
Notes:
This question provides an excellent opportunity to review inductor theory, particularly the direction of current and the polarity of voltage for an inductor when charging versus when discharging. Analysis of this circuit will be made easier by drawing a schematic diagram.
Question 4:
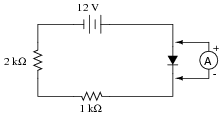
What will an ammeter (with an input resistance of 0.5 W) register when connected in parallel with the diode in this circuit?
|
|
Usually, ammeters are connected in series with the component whose current is to be measured. However, in this case a parallel connection is acceptable. Explain why, and determine the ammeter's current reading in this circuit.
Notes:
A very important point to ask your students is how they figured out the meter's indication. What circuit analysis technique did they use, and why?
Emphasize solving this problem without using a calculator to do the math. Are your students able to determine the result by estimation alone? Does the input resistance factor into the calculation significantly?
Question 5:
Suppose a very important piece of electronic equipment (nuclear reactor shutdown controls, for instance) needed to be supplied with uninterruptible DC power. For reliability's sake, this circuit gets its power from three (redundant) DC voltage sources:
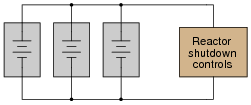
|
|
The only problem with this scenario is the possibility of one of these power sources internally short-circuiting. Describe what would happen if one of the three DC power sources developed an internal short-circuit, and explain how this problem could be avoided by placing diodes in the circuit.
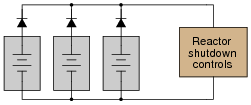
|
|
Challenge question: it would be nice if there were indicator lamps in the system to warn maintenance personnel of a shorted power supply. Is there any way you can think of to place light bulbs in this system somewhere, so that one will light up in the event of a power supply failure?
Notes:
Discuss both the nature of the problem, and of the solution, with your students. Why does the proposed solution work to eliminate power failure in the event of a short-circuit internal to one of the power sources?
Question 6:
Using a commutating diode (sometimes called a free-wheeling diode) to eliminate switch contact arcing for inductive loads in a DC circuit works well, but it has an unfortunate side-effect:
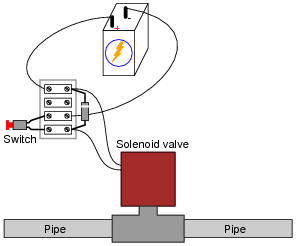
|
|
With a diode in place, the release time for the solenoid increases measurably. In other words, it takes longer for the solenoid to completely de-magnetize after the switch contacts open, than if there is no diode in the circuit.
Explain why this is, and also propose a solution for the minimizing the solenoid's release time.
Notes:
This question is an good review of inductor time constant theory, and challenges students to put their mastery of L/R time constant circuits to the test by engineering a solution for this problem.
Once a solution has been agreed upon, ask your students if the solution introduces (or re-introduces, as the case may be) any other problems in the circuit.
